Exercícios Resolvidos de Potência em Circuito CA

Ver Teoria

Exercício 4 1 2 3 5 6 7 8 9 10

Enunciado

Para o circuito da figura, .Determine a potência média absorvida pelo resistor de.

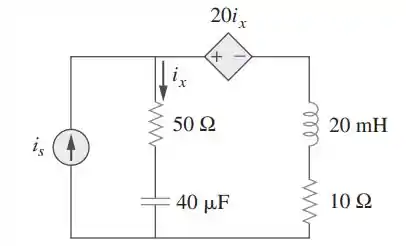
Passo 1

Vamos primeiro converter as grandezas para o domínio da frequência, ou seja,

Em seguida, calculamos as impedâncias no domínio da frequência também, sabendo que :

Para o indutor:

(lembrando que tudo tem que estar no Sistema Internacional)

Para o capacitor:

Passo 2

Agora vamos redesenhar o circuito com os valores encontrados no passo 1

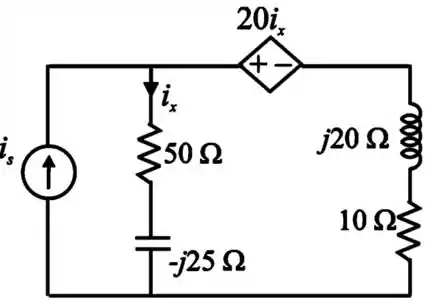
Passo 3

Vamos então aplicar a Lei das Correntes de Kirchhoff ao único nó do circuito (vamos chamar sua tensão de para encontrar o a partir da Lei de Ohm, veja:

Mas… quem é ?

Pela Lei de Ohm, , então, substituindo isso na equação anterior…

E agora sim podemos calcular o apenas substituindo esse valor:

Seu valor será

Passo 4

Então, a potência média absorvida pelo resistor de será:

Resposta

Exercícios de Livros Relacionados

7. Dado o circuito da figura 11.39 , determine a potência média absorvida pelo resistor de 10Ω .

8. No circuito da figura 11.40 determine a potência média absorvida pelo resistor de 40Ω .

6. Para o circuito da figura 11.38 , i s = 6 cos ⁡ 10 3 tA . Determine a potência média absorvida pelo resistor de 50Ω .

3. Uma carga é formada por um resistor de 60Ω em paralelo com um capacitor de 90m F . Se a carga for conectada a uma fonte de tensão v s t = 160 cos ⁡ 2000 t , determine a potência média liberada para

29- Calcule o valor eficaz da forma de onda da corrente mostrada na Figura 11.60 e a potência média liberada para um resistor de 12Ω , quando a corrente percorre o resistor.