Para o circuito abaixo, determine a impedância da carga para a transferência de potência máxima (para ). Calcule a potência máxima absorvida pela carga.
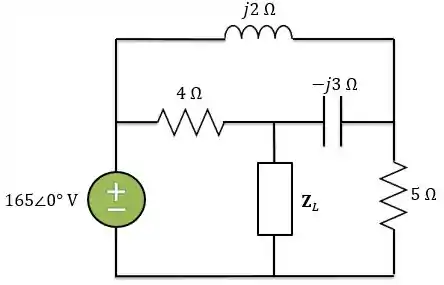
Passo 1
Quando falamos em máxima transferência de potência temos que ter em mente o teorema de Thévenin. Para começar, precisamos encontrar o circuito equivalente de Thevenin conectado a carga . Para analisarmos um circuito como o abaixo:
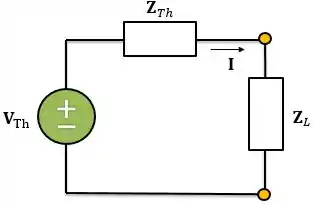
Passo 2
Para encontrar a impedância de Thevenin, desligamos a fonte de tensão, retiramos a carga e calculamos a impedância equivalente vista por seus terminais. Sempre lembrando que desligar uma fonte de tensão é o mesmo que substituí-la por um curto-circuito.
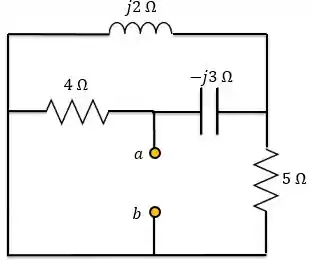
Vamos redesenhar o circuito para facilitar:
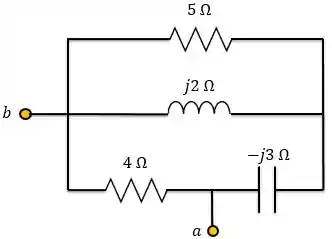
Primeiro, vamos calcular a impedância equivalente correspondente ao paralelo do resistor de com o indutor:
Então, agora temos o seguinte circuito:
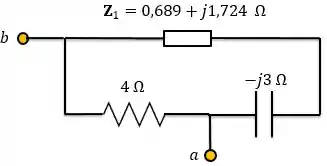
Como podemos ver, a impedância está em série com o capacitor. Portanto:
E o circuito fica assim:
Agora temos que calcular paralelo de e o resistor, que será a impedância de Thevenin.
Passando para forma retangular:
Passo 3
Como vimos na teoria, a máxima transferência de potência ocorre quando a impedância da carga é o conjugado da impedância de Thevenin, ou seja:
Então, lembrando que para obter o conjugado temos que inverter o sinal na parte imaginária, a impedância da carga será:
Passo 4
Agora falta calcularmos a potência máxima transferida, que tem a seguinte fórmula:
Para a gente poder usá-la precisamos encontrar o valor da tensão de Thevenin. Vamos fazer isso agora. Lembrando que é a tensão de circuito aberto nos terminais , vamos analisar o circuito abaixo:
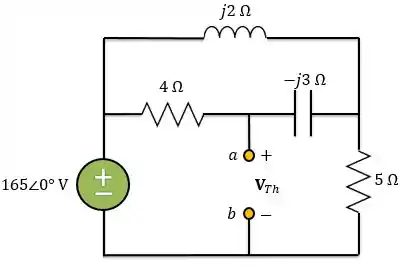
Vamos preparar o circuito para usar análise nodal:
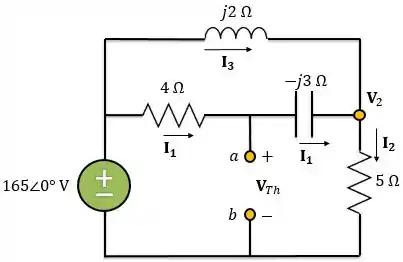
Aplicando a lei das correntes de Kirchhoff ao nó da tensão nodal :
Escrevendo em função das tensões nodais:
Passo 5
Agora que encontramos o valor de , podemos substituí-lo na equação abaixo para encontrarmos :
Estamos quase lá! Para finalmente encontrarmos , vamos aplicar a lei das tensões de Kirchhoff na malha abaixo:
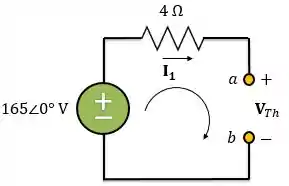
Passo 6
Agora é só lembrar que e da fórmula:
Sendo,
Ou seja, é só pegar o módulo do fasor e elevar ao quadrado.
Como,
Substituindo os valores: