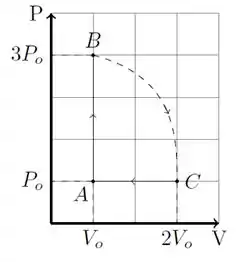
Uma certa quantidade de um gás ideal, com calor específico molar , realiza o ciclo ilustrado no diagrama da figura, onde a etapa corresponde a um processo irreversível. Seja o trabalho total realizado. Determine o trabalho, o calor e a variação da energia interna:
- Para a etapa ;
- Para a etapa ;
- Para a etapa ;
- Determine a eficiência de uma máquina de Carnot funcionando entre a menor e a maior temperaturas envolvidas neste ciclo.
Deixe suas respostas em termos de , de e de .
Passo 1
Fala galera, tudo bem? Vou ajudar você a resolver essa questão! Vamos lá?
Letra (a):
O problema pede para calcularmos o trabalho, o calor e a variação de energia interna entre os estados . Pelo gráfico dá pra ver que de para temos uma reta vertical, isso em um diagrama indica uma transformação isovolumétrica! E o que sabemos sobre ela? Que o trabalho realizado é zero!
Daqui já tiramos a primeira quantidade:
Agora vamos ver como fica a primeira lei quando temos uma transformação isométrica:
Olha só! Aqui temos que a variação de energia interna é igual ao calor!
E sabemos como se calcula o calor à volume constante:
O vale , e a variação de temperatura? Ela vai ser dada em termos das temperaturas dos estados:
Xiiii! E agora? Como vamos achar essas temperaturas? Usando a equação fundamental de estado! Se olharmos para o gráfico, vamos ver que no estado temos um valor de e para a pressão e o volume, então podemos achar a temperatura em em função dessas quantidades:
Já para o estado o volume é o mesmo, mas a pressão é triplicada, então a temperatura vai ser dada por:
Agora é só substituir no calor! Vamos lá?
Podemos cancelar e achar por fim o calor:
E a variação da energia interna? É igual ao calor! Então entre os estados e temos:
Agora precisamos fazer a mesma análise para as outras transformações, borá lá? =D
Segura na minha mão e vamos!
Passo 2
Letra (b):
Pelo gráfico dá pra ver que de para temos uma reta horizontal, isso em um diagrama indica uma transformação isobárica! E o que sabemos sobre ela? Que o calor a pressão constante é ! Então temos que para esse gás .
Agora podemos calcular o calor à pressão constante:
O vale , e a variação de temperatura? Ela vai ser dada em termos das temperaturas dos estados:
Usando de novo a equação fundamental de estado podemos achar as temperaturas! Se olharmos para o gráfico, vamos ver que no estado temos um valor de e para a pressão e o volume, então podemos achar a temperatura em em função dessas quantidades:
Já para o estado já calculamos a temperatura no passo anterior, então vou resgatar de lá:
Agora é só substituir no calor! Vamos lá?
Podemos cancelar e achar por fim o calor:
E o trabalho? Bom, numa transformação isobárica o trabalho realizado é , bem tranquilo de ser calculado:
Ufa, quase lá! Agora com o calor e o trabalho, podemos jogar tudo isso na primeira lei e descobrir a variação de energia interna, saca só (CUIDA O SINAL DO TRABALHO!):
Recapitulando: entre os estados o trabalho, o calor e a variação de energia interna valem:
Passo 3
Letra (c):
Agora vamos analisar o processo de . No enunciado diz que é um processo irreversível, mas não sabemos mais nada sobre ele. Então calcular o trabalho por aí é um pouco complicado. Vamos pensar no processo como um todo. O trabalho total realizado é sempre a soma dos trabalhos de cada transformação, certo? E temos que o trabalho total é , então temos:
E já sabemos que é zero, pois se trata de uma transformação isométrica, e também sabemos que . Então vamos substituir esses valores e deixar o trabalho de em termos do trabalho total e das quantidades e :
E é essa a resposta!
E quanto ao calor? Sabemos que em um ciclo, a variação de energia interna é zero, pois temos o retorno do sistema à temperatura inicial. Sendo assim, em um ciclo, todo calor é convertido em trabalho . E o calor total? Bom, ele é a soma dos calores envolvidos em cada transformação. Então com o mesmo espírito da resolução do trabalho de , vou fazer de forma similar para o calor.
Vamos primeiro achar o calor total
Como já falei ali em cima, em um ciclo , e os calores já foram calculados anteriormente, então vou resgatar os resultados e colocar ali em cima:
Por fim a variação de energia interna! Eu sempre a deixo por último porque daí é só jogar os resultados do calor e do trabalho na primeira lei! Só cuuuuida o sinal do trabalho!
Aqui o valor do trabalho total some e teremos a resposta em termos da pressão e do volume iniciais:
Recapitulando, entre os estados e os valores de calor, trabalho e variação de energia interna são:
Passo 4
Letra (d):
Agora o problema pede o rendimento dessa máquina. A menor temperatura é no estado e vale:
E a maior? É no estado e essa temperatura vale:
O rendimento de uma máquina é:
Assim o rendimento é .
Beleza?
Pronto pra próxima questão? =)