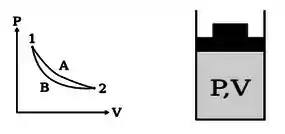
Um gás ideal está confinado num cilindro com pistão que pode se mover sem atrito. O gás pode sofrer as transformações ou do estado para o estado . É correto afirmar que (cuidado com o sinal):
- sobre gás A sobre o gás B
- sobre gás A sobre o gás B
- sobre gás A sobre o gás B
- sobre gás A sobre o gás B
- sobre gás A sobre o gás B
Passo 1
Então, nós estamos acostumados a convenção de sinais que considera positivo o trabalho realizado PELO gás. Ou seja: expansões têm trabalho positivo, compressões trabalho negativo.
Pelo gráfico vemos que os processos A e B são compressões. Então o trabalho realizado PELO gás é negativo nos dois casos.
Além disso, nós podemos calcular o trabalho pela área abaixo da curva.
Como a área abaixo da curva A é maior que a área abaixo da curva B, o trabalho vai ser maior, veja bem, EM MÓDULO, pro processo A. Então o que nós vamos ter é:
Mas:
Porque o trabalho em A é MAIS NEGATIVO, a área abaixo da curva é maior. Tendeu?
E como fica o trabalho realizado SOBRE O GÁS? Na nossa convenção, é só trocar o sinal.
E aí ficaremos com:
Guarde isso!
Passo 2
Sabemos lá da teoria da primeira Lei de Termodinâmica, que a variação da Energia interna é uma função de estado, que ela só depende do estado final e inicial, não importando o caminho que ela percorreu. No nosso exercício, os dois caminhos vão do estado para o estado , ou seja, o ponto inicial e final é o mesmo. Então, concluímos que:
e pela Primeira Lei da Termodinâmica, pode-se se reescrever essa igualdade como:
Como descobrimos lá no início que:
Podemos concluir que:
Repare aqui que usamos:
Porque estamos fazendo o trabalho SOBRE o gás. Se fosse o trabalho PELO GÁS o sinal de W mudaria nessa fórmula.
Resposta
Letra B.