Considere dois processos reversíveis distintos que levam um gás ideal de um estado inicial para um estado final que consistem de:
I - Uma expansão isotérmica.
II - Uma expansão adiabática seguida de uma expansão isobárica.
Quanto à variação de energia interna, trabalho realizado pelo gás e calor recebido pelo gás, pode-se dizer que:
(a)
(b)
(c)
(d)
(e)
Passo 1
Opa! Vamos pensar juntos!
Primeiro em relação a energia interna, ela é uma função de estado, isso quer dizer que não importa o caminho, a variação da energia interna depende apenas dos estados inicial e final. E como, no nosso caso esses estados são os mesmos para e para , temos que
Passo 2
Agora, em relação ao trabalho, vamos lembrar de algumas coisas. O trabalho é dado pela área abaixo da curva do gráfico . E é bom lembrarmos também que a curva adiabática tem um decaimento mais rápido do que a curva isoterma. Então, isso quer dizer que um diagrama , para o nosso caso, ficaria assim:
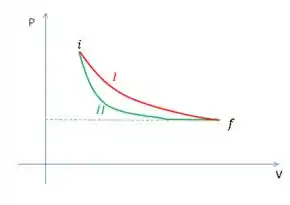
Notem que a área sob o gráfico da curva é maior do que o da curva , então
Passo 3
E pra fechar, em relação as trocas de calor.
Bom, já falamos de energia interna e de trabalho. Isso te lembra alguma coisa? Primeira lei da termodinâmica, que relaciona todas essas grandezas!
Como vimo,
Vimos também que . Então, para manter a igualdade válida, temos que
Resposta
Letra c)