O apoio é composto por um poste sólido de latão vermelho C83400 embutido em um tubo de aço inoxidável 304. Antes da aplicação da carga, a folga entre essas duas partes é . Dadas as dimensões mostradas na figura, determine a maior carga axial que pode ser aplicada à tampa rígida sem provocar o escoamento de qualquer um dos materiais.
Dados: , , & .
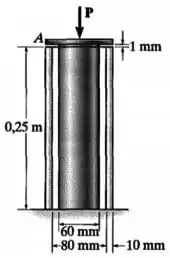
Dica do expert: Em um exercício com folga entre as peças como esse, é bom verificar se as peças vão chegar a se encostar mesmo ou não.
Passo 1
Nesse exercício, temos:
- Um poste de latão com comprimento inicial , módulo de elasticidade , e diâmetro ;
- E um tubo de aço com comprimento inicial , módulo de elasticidade , diâmetro interno e diâmetro externo .
Se o poste de latão for comprimido o suficiente pela carga , a sua face superior vai começar a se apoiar também no tubo de aço.
E o que é que o exercício quer?
Ele quer que a gente descubra a maior carga que pode ser feita sem que as tensões nos materiais ultrapassem as suas tensões de escoamento:
Agora, em um exercício com uma folga entre as peças como esse, é importante verificar se é possível fazer a folga desaparecer.
No nosso caso, precisamos verificar se a variação de comprimento de necessária para acabar com a folga já não é suficiente para fazer o poste de latão escoar.
Caso não seja, aí vamos ter a face superior do poste se apoiando no tubo de aço, e o problema vai se tornar um problema estaticamente indeterminado.
Para resolver esse problema estaticamente indeterminado, vamos ter que estudar o equilíbrio de forças nas peças e a compatibilidade das variações de comprimento de cada peça.
No nosso caso, temos que para cada milímetros de compressão no tubo de aço, o poste de latão vai ter que ter tido a mesma compressão mais a folga de .
Dessa forma, a nossa equação de compatibilidade vai ser:
Passo 2
Então, antes de podermos declarar que o exercício é estaticamente indeterminado, precisamos verificar se o latão já não vai escoar antes de encostar no tubo de aço.
Para tanto, vamos avaliar qual é a tensão no latão correspondente à variação de comprimento .
Para tanto, podemos usar a Lei de Hooke e a definição de deformação :
Juntando essas duas equações, temos que:
Para o poste de latão, isso significa que:
Sabemos que e que .
Além disso, para avaliar qual é a tensão no latão correspondente à variação de comprimento , devemos substituir .
Substituindo esses valores e calculando tudo, encontramos que:
Vemos que essa tensão é bem maior que a tensão de escoamento do latão, .
Isso significa que a carga máxima permitida no nosso conjunto vai ocorrer enquanto o latão ainda não encostou no tubo de aço.
Sendo assim, não nos precisamos nos preocupar com toda a parte estaticamente indeterminada do exercício para resolver ele!
Passo 3
Para determinar a carga máxima que pode ser aplicada no poste, vamos usar a condição:
(Ou seja, queremos que a tensão normal no latão seja menor ou igual à tensão de escoamento desse material.)
Usando a fórmula da tensão normal média para descrever a tensão no latão, a nossa condição fica assim:
Como só queremos avaliar a intensidade da tensão , não precisamos nos preocupar com o sinal da força interna normal .
Se a única força atuando no poste de latão é a força de compressão, vamos ter então que a força normal vai ter uma intensidade .
Além disso, a área da seção transversal do poste pode ser encontrada a partir do diâmetro do poste usando a fórmula:
Dessa forma, a nossa condição fica assim:
Isolando , temos que:
Substituindo os valores e , temos que:
Calculando tudo, isso nos diz que:
Ou seja, a força máxima que pode ser aplicada no poste é:
E assim está resolvido o exercício!
Caso não tivéssemos verificado se o poste ia encostar no tubo de aço, poderíamos acabar não percebendo isso depois e resolvendo o exercício de uma forma errada.