A barra rígida é suportada por quatro fios idênticos. Determine a tração em cada fio causada pela carga mostrada.
Passo 1
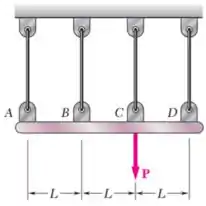
Temos uma barra rígida carregada com uma força e sustentada por fios igualmente espaçados por uma distância .
Fazendo o diagrama de corpo livre dessa barra, vemos que a força é equilibrada pelas forças de tração dos fios:
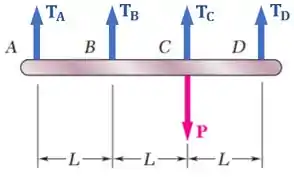
O exercício quer saber o valor dessas trações , , e .
Para fazer isso, o primeiro passo é aplicar as condições de equilíbrio na barra para tentar relacionar as forças de tração com a carga .
Mas só temos duas equações de equilíbrio que podem ser usadas aqui (o equilíbrio de forças na vertical e o equilíbrio de momentos).
Ou seja, as condições de equilíbrio não serão o suficiente para encontrar as quatro trações desconhecidas.
Para complementar as equações de equilíbrio, vamos precisar imaginar como vão ser as variações de comprimento .
Assim, vamos conseguir encontrar as equações de compatibilidade desse problema.
Passo 2
Vamos começar aplicando as condições de equilíbrio na barra !
Primeiro, podemos aplicar o equilíbrio de forças na vertical:
Fazendo esse somatório, encontramos que:
Ou seja:
Em seguida, podemos aplicar o equilíbrio de momentos.
Escolhendo avaliar os momentos em relação ao ponto , temos:
Olhando para o diagrama de corpo livre que fizemos no Passo 1, conseguimos identificar os seguintes momentos em relação ao ponto :
- Um momento no sentido horário () gerado pela tração com um braço ;
- Outro momento no sentido horário (), dessa vez gerado por e com um braço ;
- E um momento no sentido anti-horário () gerado por com um braço .
Dessa forma, o nosso somatório de momentos fica assim:
Dividindo tudo por e isolando , temos que:
Passo 3
Se temos trações desconhecidas mas somente equações de equilíbrio, precisamos encontrar equações de compatibilidade para podermos determinar todas as trações.
Para tanto, vamos imaginar como as variações de comprimento de cada fio vão afetar o posicionamento da nossa barra:
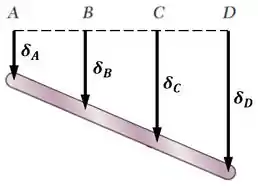
A partir dessas variações, podemos desenhar três triângulos:
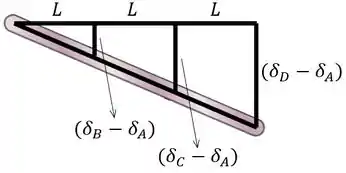
Fazendo uma semelhança de triângulos entre o triângulo menor e o triângulo médio, temos que:
Multiplicando tudo por , isso fica assim:
Isolando , encontramos a nossa primeira equação de compatibilidade:
Fazendo outra semelhança de triângulos, dessa vez entre o triângulo menor e o triângulo maior, temos que:
Multiplicando tudo por e isolando , encontramos nossa segunda equação de compatibilidade:
Passo 4
Do jeito como encontramos no passo anterior, as equações de compatibilidade e ainda não são muito úteis.
Para que elas sejam úteis, precisamos usar elas para relacionar as trações nos fios.
Então vamos pensar...
A variação de comprimento em um fio pode ser obtida pela fórmula:
Nos nossos fios, a força interna normal vai ser sempre igual à tração , ou seja:
Agora, o termo é igual para todos os fios, afinal, todos os fios são idênticos, a única coisa que muda entre eles é a tração .
Podemos dizer que esse termo é uma constante de tal forma que a relação abaixo vale para qualquer um dos nossos fios:
Sendo assim...
As equações de compatibilidade podem ser reescritas em função das trações em cada fio.
A equação pode ser reescrita assim:
O que significa que:
Da mesma forma, a equação vai significar que:
Passo 5
Agora sim temos equações relacionando as quatro trações desconhecidas , , e !
Com isso, só falta combinar essas equações para encontrar o valor individual de cada uma.
Primeiro, unindo a Equação 2 e a Equação 4, temos que:
Passando tudo para a esquerda, temos:
Isolando , encontramos que:
Vamos guardar essa relação como a Equação 5! 😊
Além disso, podemos pegar a Equação 1:
E substituir nela as Equações 2 e 3:
Arrumando isso, encontramos que:
Substituindo a Equação 5 aqui, isso fica assim:
O que significa que:
Encontrado , podemos usar a Equação 5 para encontrar :
Encontrados e , podemos usar a Equação 2 para encontrar :
E, finalmente, encontrados , e , podemos usar a Equação 1 para encontrar :
E assim está resolvido o nosso exercício!