A carga de deve ser suportada pelos dois cabos verticais de aço para os quais . Se os comprimentos originais dos cabos e forem e respectivamente, determine a força desenvolvida em cada cabo depois da suspensão da carga. Cada cabo tem área de seção transversal de .
Dados: .
Passo 1
O que está acontecendo?
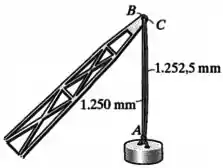
Os cabos e possuem comprimentos originais e , um módulo de elasticidade e uma área de seção transversal .
Através de forças de tração e , eles suportam juntos a carga de :
Inicialmente, os cabos têm comprimentos diferentes.
Mas uma vez que os cabos são carregados com o peso, eles:
- Sofrem variações de comprimento e ;
- E passam a compartilhar o mesmo ponto , o que significa que eles precisam ter comprimentos finais iguais.
E o que é que o exercício quer?
Ele quer saber o valor dessas forças de tração e desenvolvidas nos cabos.
Para encontrar essas duas forças, podemos recorrer ao equilíbrio de forças no ponto e a uma equação de compatibilidade entre as variações de comprimento e .
Passo 2
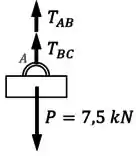
Vamos começar fazendo um diagrama de corpo livre do ponto :
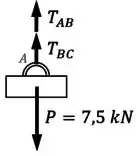
Com isso, podemos agora aplicar as condições de equilíbrio no ponto .
Para esse ponto, a única condição de equilíbrio disponível é o equilíbrio de forças na vertical:
Fazendo esse somatório de forças, temos:
O que significa que:
Essa única equação não é suficiente para que a gente possa encontrar as incógnitas e , então vamos precisar também de uma equação de compatibilidade.
Passo 3
Para encontrar uma equação de compatibilidade, precisamos pensar em como os cabos vão se deformar.
No passo 1, vimos que os dois cabos devem ter os mesmos comprimentos finais :
Isso significa que:
Passando para a esquerda e para a direita, temos:
Substituindo e , vamos encontrar que:
Essa é a nossa equação de compatibilidade.
Passo 4
Para que a equação de compatibilidade seja útil para a gente, vamos precisar descrever as variações de comprimento e em função das trações e .
Para tanto, podemos usar a fórmula:
No caso dos nossos cabos, a força interna normal vai ser sempre igual à tração , ou seja:
Dessa forma, a nossa equação de compatibilidade fica assim:
Multiplicando os dois lados por , temos que:
Isolando , encontramos:
Passo 5
Agora, podemos pegar a equação que encontramos ao final do passo 2:
E substituir a expressão que acabamos de encontrar para :
Com essa expressão, conseguimos isolar e encontrar a tração desconhecida !
Multiplicamos os dois lados por :
Passamos para o outro lado e colocamos em evidência:
E finalmente isolamos :
Substituindo:
- E
Vamos encontrar que:
Encontrado o valor de uma tração, conseguimos encontrar o valor da outra.
Para isso, pegamos novamente a equação que veio do equilíbrio de forças:
Isolamos :
E substituímos e para encontrar que:
E assim está resolvido o exercício!