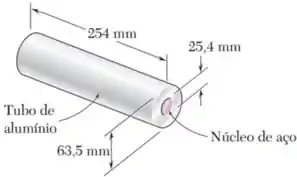
Forças de compressão centradas de são aplicadas em ambas as extremidades do conjunto mostrado na figura por meio de placas rígidas. Sabendo que e , determine as tensões normais no núcleo de aço e no tubo de alumínio e a deformação do conjunto.
Passo 1
Nesse exercício, temos:
- Um núcleo de aço com diâmetro e módulo de elasticidade ;
- E um tubo de alumínio com diâmetro interno , diâmetro externo e módulo de elasticidade .
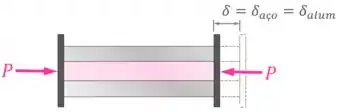
Essas duas peças têm um comprimento original e estão sendo comprimidas por uma força por meio de placas rígidas nas suas extremidades:

Além disso, ainda temos que essa compressão por meio de placas rígidas vai causar aço e no alumínio variações de comprimento e iguais:
No item , o exercício quer que a gente encontre as tensões normais em cada peça, que vão ser dadas pela fórmula da tensão normal média .
O primeiro passo vai ser fazer um DCL (diagrama de corpo livre) das peças para identificar as forças atuando no aço e no alumínio.
Como as condições de equilíbrio não vão ser suficientes para achar as incógnitas desse DCL, vamos ter que usar também a condição de compatibilidade .
Finalmente, uma vez que tivermos encontrado as forças atuando em cada peça, vamos poder calcular as tensões nelas.
Já no item , o exercício quer saber a deformação do conjunto.
Como as duas peças tem comprimentos originais e variações de comprimento iguais, a deformação nelas vão ser iguais.
Assim, podemos usar a tensão e o módulo de elasticidade de qualquer uma das peças para encontrar a deformação do conjunto usando a Lei de Hooke .
Passo 2
Começamos fazendo o diagrama de corpo livre das peças presentes no exercício:

Com isso, percebemos que uma porção da força de compressão é suportada pelo aço e outra porção é suportada pelo alumínio.
Aplicando as condições de equilíbrio para as placas rígidas, temos que o somatório de forças na horizontal dessas placas deve ser igual a zero:
O que significa que:
O que já era esperado.
Mas infelizmente, essa única equação não é o suficiente para que a gente consiga encontrar as incógnitas e .
Então vamos precisar de uma equação de compatibilidade para complementar essa equação.
Passo 3
Pensando em como as nossas peças vão se deformar:
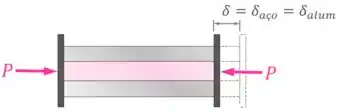
Conseguimos identificar a equação de compatibilidade:
Agora, essa equação de compatibilidade escrita dessa forma não tem muita utilidade para a gente.
Precisamos conseguir descrever as variações de comprimento e em função dos carregamentos nessas peças.
Mas lembra aí!
Existe uma fórmula que nos fornece essas variações de comprimento a partir do carregamento em uma peça:
(É a fórmula que vem da combinação das definições da tensão normal média e da deformação com a Lei de Hooke .)
Aplicando essa fórmula para as nossas variações de comprimento, temos que:
Nessa equação, conseguimos observar que:
- A força normal vai ser igual a menos a força de compressão no aço;
- Da mesma forma, a força normal no alumínio vai ser ;
- Tanto o núcleo de aço quanto o tubo de alumínio possuem o mesmo comprimento inicial , então os termos e vão se cortar;
- A área do núcleo de aço pode ser encontrada em função de seu diâmetro usando a fórmula ;
- E, por último, a área do tubo de alumínio é igual à área do círculo externo menos a área do círculo interno .
Fazendo todas essas operações, aquela expressão fica assim:
Multiplicando os dois lados por , temos:
O que significa que:
Substituindo os valores , , e e calculando tudo, encontramos que:
Passo 4
Agora que temos uma relação entre as incógnitas e além da relação que veio do equilíbrio de forças...
...conseguimos unir essas duas relações para encontrar os valores de e .
Substituindo na relação que veio do equilíbrio de forças, temos que:
O que significa que:
Como é igual a , encontramos que:
E, como , isso significa que:
Passo 5
Agora que conhecemos os carregamentos em cada peça, podemos calcular as tensões normais médias para cada peça.
Para o núcleo de aço, temos:
Já vimos anteriormente que e que , então temos que:
Substituindo os valores e , isso dá:
Como esse número é um pouco pequeno, podemos reescrever essa tensão em :
Já para o tubo de alumínio, temos:
No passo 3, vimos que e , então:
Substituindo , e e calculando tudo, encontramos:
E, finalmente, reescrevendo em encontramos que:
Passo 6
Resolvido o item , seguimos para o item !
No item , queremos saber a deformação do conjunto, que é a deformação sofrida tanto pelo aço quanto pelo alumínio.
Escolhendo por aplicar a Lei de Hooke para o aço, temos:
Isolando :
Substituindo e , temos que:
Calculando isso, encontramos nossa resposta:
Se quisermos, ainda podemos escrever essa resposta com uma unidade de deformação como ou .