O tubo de aço A-36 tem raio externo de e raio interno de . Se ele se ajustar exatamente entre as paredes fixas antes de ser carregado, determine a reação nas paredes quando for submetido à carga mostrada.
Dados: .
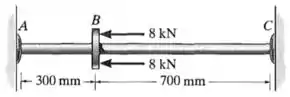
Passo 1
O que está acontecendo?
Temos um tubo de raio externo e raio interno .
Sendo assim, a área da seção transversal desse tubo vai ser dada pela diferença entre as áreas dos círculos com o raio externo e com o raio interno:
Além disso, o tubo possui um módulo de elasticidade e é dividido em dois segmentos, e , com comprimentos originais e .
Inicialmente, o tubo se ajusta exatamente nas paredes e não existe nenhuma reação nas paredes.
Mas, quando o tubo é submetido à carga mostrada, ele passa a sofrer reações das paredes em e em para que ele se mantenha em equilíbrio:
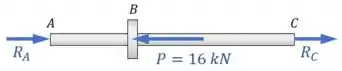
Beleza, e o que é que o exercício quer?
Ele quer saber o valor das reações desconhecidas e .
Como são duas reações desconhecidas, mas só uma condição de equilíbrio está disponível para a gente (o equilíbrio de forças na horizontal), esse tubo é estaticamente indeterminado.
Isso significa que nós vamos precisar de uma equação de compatibilidade para resolver o exercício.
Para achar essa equação de compatibilidade, podemos estudar a variação de comprimento de cada segmento do tubo.
(Também poderíamos usar o método de análise de força, mas seria mais demorado...)
Passo 2
Da mesma forma que em muitos outros exercícios, vamos começar fazendo um diagrama de corpo livre da peça:
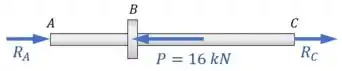
Feito o DCL, aplicamos as condições de equilíbrio.
Nesse caso, a única condição disponível é o equilíbrio de forças na vertical:
Fazendo esse somatório, encontramos que:
Vamos guardar essa equação para depois!
Passo 3
A relação não é o suficiente para encontrar os valores das reações, então precisamos de uma equação de compatibilidade.
Para encontrar essa equação, vamos observar as variações de comprimento em cada segmento da peça!
O segmento vai sofrer uma variação de comprimento enquanto que o segmento vai sofrer uma variação de comprimento .
A soma dessas duas variações vai ser a variação de comprimento total da peça:
Mas como as paredes não se movem, a variação de comprimento total da peça deve ser nula, de tal forma que:
O que significa que:
Essa é a nossa equação de compatibilidade!
Passo 4
A equação de compatibilidade da forma que encontramos no passo anterior não tem muita utilidade para a gente.
Precisamos conseguir descrever as variações de comprimento e em função dos carregamentos na peça.
Para tanto, podemos usar a fórmula:
Aplicando essa fórmula para cada segmento e tendo em mente que os dois segmentos tem módulos de elasticidade e áreas de seção transversal iguais, temos que:
Cortando com , e substituindo e , isso fica assim:
O que significa que:
Passo 5
Conseguimos relacionar os carregamentos internos nos segmentos da peça com a relação , mas precisamos mesmo é relacionar as reações na peça.
Para tanto, podemos fazer uma análise de esforços internos na peça para definir as forças internas normais em função das reações .
Para as seções entre e , temos:

Fazendo o equilíbrio de forças na horizontal, temos que:
O que significa que:
Já para as seções entre e , essa análise fica assim:

Mais uma vez aplicamos o equilíbrio de forças na horizontal:
Para encontrar dessa vez que:
Passo 6
Pronto, agora podemos voltar na relação que tínhamos encontrado:
E substituir e :
Simplificando, essa expressão fica assim:
Por fim, para resolver o exercício, precisamos substituir essa relação na Equação 1 que tínhamos guardado:
Fazendo essa substituição, temos:
Isolando , encontramos que:
O que dá:
E, como , temos que:
E assim está resolvido o nosso exercício!