A coluna de aço A-36 é usada para suportar as cargas simétricas dos dois pisos de um edifício. Determine o deslocamento vertical de sua extremidade, , se , e a coluna tiver área de seção transversal de .
Dados: .
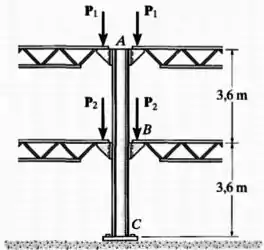
Passo 1
Os pares de forças e estão comprimindo a coluna , que possui uma área de seção transversal e um módulo de elasticidade .
O exercício quer saber o deslocamento da extremidade .
Para encontrar esse deslocamento, podemos:
- Encontrar as forças normais e as variações de comprimento nos trechos e . Nesse caso, vamos ter que ;
- Ou calcular individualmente as variações de comprimento e causadas pelos pares de forças e , respectivamente, e usar o princípio da superposição para definir que .
Aproveitando esse exercício para treinar o princípio da superposição, vamos utilizar o segundo método!
Passo 2
Aplicando o princípio da superposição, podemos calcular individualmente as deformações e , causadas pelos pares de forças e , respectivamente.
E, depois, podemos somar esses efeitos para encontrar a deformação total na coluna:
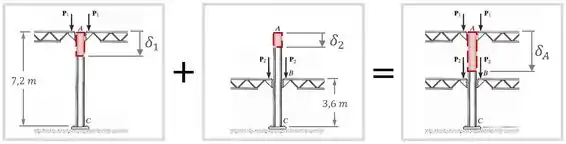
Dessa superposição de efeitos, encontramos que:
Então nos resta encontrar as deformações e causadas por cada carregamento.
Passo 3
Para encontrar a deformação causada pelas forças , vamos pensar na situação em que só as forças estão atuando:
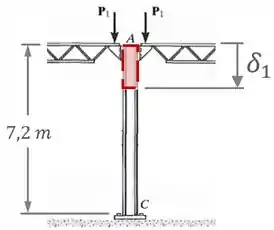
Nesse caso, a coluna vai ser um grande segmento de comprimento , área de seção transversal e módulo de elasticidade .
Além disso, como as únicas forças atuando são as duas forças de compressão, vamos ter que a força normal na coluna vai ser .
Daí que para encontrar a variação de comprimento , podemos usar a fórmula , de tal forma que:
Passo 4
De forma análoga ao passo passado, vamos agora pensar no caso em que somente as forças estão atuando:
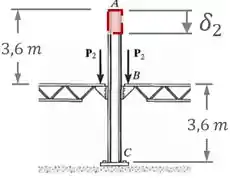
Nesse caso, a coluna vai ser composta por dois segmentos e , ambos com uma área de seção transversal , módulo de elasticidade e comprimento .
Dessa forma, a variação de comprimento na coluna vai ser igual à soma das variações de comprimento de cada segmento:
Fazendo essa soma, temos que:
Agora, enquanto que o segmento vai ter uma força normal , o segmento não vai estar carregado, e vai ter assim uma força normal nula.
Com isso, encontramos que:
Passo 5
Por fim, aplicando a fórmula que tínhamos encontrado anteriormente para superposição dos efeitos, temos que:
Substituindo as expressões encontradas para e :
Arrumando, isso fica assim:
Substituindo , , , , e , temos que:
Para calcular isso, precisamos prestar atenção nas unidades.
Nesse caso, podemos nos lembrar que é o mesmo que . Assim, as unidades e se cortam e o resultado final sai em , que é a unidade que vai sobrar.
Calculando tudo, encontramos então que:
Esse número é bem pequeno, então podemos reescrevê-lo em na hora de darmos a resposta: