A barra de aço abaixo está distante 2cm da parede a sua direita. Determine as reações da parede quando a barra for submetida ao carregamento mostrado abaixo. Use e considere a área da seção como uma área quadrada de dimensões (25x25)cm.
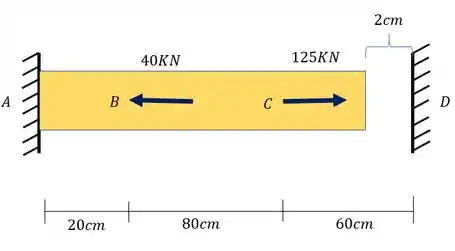
Passo 1
Como podemos ver, nesse tipo de questão precisamos determinar as reações de apoio. Para determinarmos essas reações de apoio precisamos saber se o nosso problema é isostático ou se é um problema estaticamente indeterminado. Como temos duas paredes no nosso problema, podemos desconfiar que talvez seja a segunda opção.
Para termos certeza que se trata de um problema estaticamente indeterminado, precisamos definir o diagrama de corpo livre e fazer o balanceamento entre o número de incógnitas e o número de equações, então vamos lá
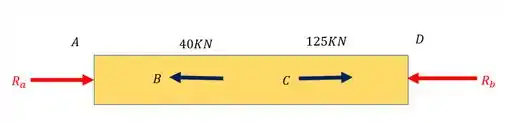
Fazendo o somatório de forças teremos que
Vamos considerar para direita positivo e para esquerda negativo, se no final a resposta tiver sinal negativo significa que a direção que escolhemos na verdade é contraria, logo teremos que
Como podemos ver temos duas incógnitas ( e uma única equação (), logo de fato se trata de um problema estaticamente indeterminado. Sabemos então, que para resolve-lo precisamos do que chamamos de equação de compatibilidade.
Passo 2
Temos que lembrar que a nossa equação de compatibilidade terá como fórmula a nossa equação de deformação total, dada por
Mas onde ela será usada?
Ai que entra a nossa relação de deformação, ou seja, a deformação da nossa barra deve ser igual a deformação total máxima que ela pode ter, que pode ser dada por
O que precisamos saber primeiro: a nossa barra sofre um deslocamento total máximo de 2cm
O que devemos saber por segundo é que a deformação do trecho AD é composto de três parcelas, uma do trecho AB, uma do trecho BC e por fim do trecho CD. Logo podemos escrever a nossa equação de compatibilidade como.
Colocando tudo em termos do que já temos e também usando a nossa fórmula de deformação total teremos que
Sabemos que como a barra é homogênea, tanto a área quanto o módulo de elasticidade são iguais nos três trechos. Também sabemos facilmente determinar o valor de cada comprimento que é dado no desenho. Então o que falta é apenas determinar o valor dos normais.
Passo 3
Como só falta determinar o normal, basta apenas que cortemos as barras e façamos o equilíbrio da nossa peça.
Primeiro normal do trecho AB

Fazendo o equilíbrio teremos que
Normal do trecho BC
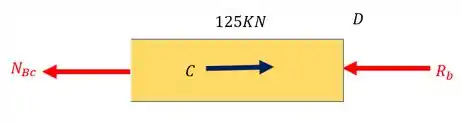
Fazendo o equilíbrio teremos que
Normal do trecho CD
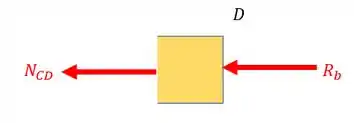
Fazendo o equilíbrio teremos que
Passo 4
Agora que já temos os valores dos normais vamos substituir na nossa equação
Agora vamos isolar os valores de
Podemos multiplicar todos os termos por
Isolando teremos que
Agora é só calcularmos o valor de
Passo 5
Sabemos que
Quando multiplicarmos EA teremos a resposta em KN
Substituindo teremos que
Como já sabemos qual é a nossa primeira equação, basta substituir nela para descobrimos o valor de