Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Propagação das Ondas Eletromagnéticas

Ver Teoria
Exercício 81234567910111213141516171819

Enunciado

O campo elétrico de uma onda eletromagnética plana monocromática que se propaga no vácuo é dado por E → z , t = E 0 sin ⁡ 2 π β z + γ t i ^ , onde β > 0 e γ > 0 são constantes.

(a) (0,5 ponto) Determine a direção e o sentido de propagação da onda. Calcule o comprimento de onda e a frequência desta onda em função das constantes β e γ .

(b) (0,5 ponto) Que relação deve haver entre β e γ para que o campo E → ( z , t ) satisfaça a equação de ondas eletromagnéticas no vácuo?

(c) (0,5 ponto) Expresse o campo magnético B → em função de E 0 , β , γ e da velocidade da luz no vácuo c .

(d) (1,0 ponto) Calcule o vetor de Poynting instantâneo e a densidade de energia média desta onda.

Passo 1

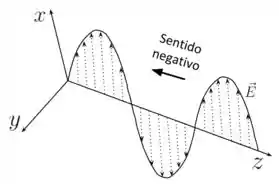
Sabemos que o vetor campo elétrico é dado por E → z , t = E 0 sin ⁡ 2 π β z + γ t i ^ . Desta expressão, é possível perceber que a onda se propaga na direção do eixo z , no sentido negativo, como na figura abaixo (para t = 0 ) .

Passo 2

Sabemos que a expressão genérica para uma onda que se propaga na direção do eixo z , no sentido negativo é dada por E → z , t = E 0 sin ⁡ k z + ω t i ^ , onde k é o número de onda e ω , a frequência angular.

Podemos comparar diretamente com a expressão do campo dada no enunciado. Temos:

k = 2 π β ,

ω = 2 π γ .

O comprimento de onda λ pode ser obtido de k a partir da expressão λ = 2 π k . A frequência f pode ser obtida de ω a partir da expressão f = ω 2 π . Assim sendo, temos:

λ = 2 π k = 1 β = β - 1 ,

f = γ .

Passo 3

A equação do campo de uma onda eletromagnética se propagando no vácuo é dada por:

∂ 2 E ( z , t ) ∂ z 2 = 1 c 2 ∂ 2 E z , t ∂ t 2 .

Substituindo E z , t = E 0 sin ⁡ 2 π β z + γ t na expressão acima, temos:

∂ ∂ z E 0 2 π β cos ⁡ 2 π β z + γ t = 1 c 2 ∂ ∂ t E 0 2 π γ cos ⁡ 2 π β z + γ t ,

- E 0 2 π β 2 sin ⁡ 2 π β z + γ t = - 1 c 2 E 0 2 π γ 2 sin ⁡ 2 π β z + γ t ,

β 2 = 1 c 2 γ 2 ,

β = γ c .

Passo 4

Para calcular o módulo do campo B → , utilizamos a seguinte expressão:

B = E c = E 0 c sin ⁡ 2 π β z + γ t .

Bem, sabemos que E → se propaga na direção do eixo z no sentido negativo, ou seja, - k ^ . Como E → × B → fornece a direção e o sentido da propagação da onda, ou seja, - k ^ , B → deve ter a direção do eixo y no sentido negativo, ou seja, - j ^ . Sacou?

Portanto,

B → = - E 0 c sin ⁡ 2 π β z + γ t j ^ .

Resposta

(a) O comprimento de onda λ e a frequência f desta onda são dados por:

λ = β - 1 ,

f = γ .

(b) A relação entre β e γ é dada por:

β = γ c .

(c) O campo magnético B → é dado por:

B → = - E 0 c sin ⁡ 2 π β z + γ t j ^ .

Exercícios de Livros Relacionados

Corrente de deslocamento não uniforme. A Fig. 32-29 mostra uma região circular de raio R = 3,00c m na qual existe uma corrente de deslocamento uniforme i d dirigida para fora do papel. O módulo da cor
Densidade de corrente de deslocamento uniforme. A Fig. 32-30 mostra uma região circular de raio R = 3,00c m na qual existe uma corrente de deslocamento dirigida para fora do papel. A corrente de deslo
O módulo do campo elétrico entre as duas placas paralelas circulares da Fig 32-32 é E = 4,0 ⋅ 10 5 - ( 6,0 ⋅ 10 4 t ) , com E em volts por metro e t em segundos. No instante t = 0 , E → aponta para ci
Romer estava observando os eclipses da Lua de Jupiter lo com a esperanca que elas servissem como um relogio altamente preciso que seria independente da longitude.(Antes do GPS,este relógio era necessa
Mostre que qualquer funcdo da forma y(x,t)=f(x-t) ouy(r,1)=g(r+ut)satisfaz a equacio de onda(Equacio 30-7).