Uma onda eletromagnética plana e monocromática possui campo magnético , vetor número de onda e frequência angular . O campo elétrico dessa onda vale?
Passo 1
Em uma onda eletromagnética, temos que:
Onde é o vetor que dá a direção e o sentido de propagação da onda (dividimos o campo elétrico e o magnético pelos seus módulos porque só queríamos a direção e sentido deles!).
Isso significa, pela regra da mão direita, que eles TEM QUE SER ASSIM:
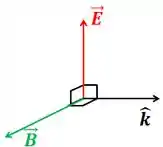
“Mas eu posso desenhar isso igual, mas colocando o deitado ali no lugar de ?”
“NÃAAAAOOOOOOO!!!!!!!”
Eles têm que estar na ordem que eu coloquei aí. Você pode ir girando todos juntos, mas nunca tirar da ordem.
Passo 2
Do nosso desenho no passo anterior, a regra da mão direita também diz pra gente que:
Agora, vamos parar com essa de ficar dividindo pelo módulo, porque:
Assim:
Agora, o produto vetorial tem a incrível propriedade de:
Logo:
Acabou? NÃO! Nota que nas respostas, nós não temos , mas sim !
“Faz diferença se você decidiu usar um chapéu ou um boné?”
Faz. O vetor é o vetor que dá não apenas a direção e o sentido da onda, mas também o seu número de onda . (é muito “k”).
Agora, vem a sacadinha: Temos duas formas de escrever a velocidade da onda.
Show, então vamos reescrevernosso resultado.
Pronto, agora sim podemos dizer que a resposta é a letra .
Resposta
Letra