Exercícios Resolvidos de Propagação das Ondas Eletromagnéticas

Exercício 15 1 2 3 4 5 6 7 8 9 10 11 12 13 14 16 17 18 19

Enunciado

Origem do Exercício

O campo magnético de uma onda propagante é dado por . A direção de polarização dessa onda é:

Passo 1

Por convenção, a direção de polarização de uma onda eletromagnética é a mesma que a direção de vibração do campo elétrico.

Embora o enunciado não tenha nos dado ela direto, ele nos deu a direção de vibração do campo magnético, que vai ser perpendicular a ela.

Assim, temos dois caminhos que podemos seguir para resolver esse problema.

Passo 2

O primeiro caminho é considerar que a direção do campo elétrico é do tipo

Fazemos o produto escalar com a direção do campo magnético e igualamos a zero. Isso daria:

Ou seja:

Isso significa que se fixarmos , temos o . Essa relação entre e define a nossa direção. A escolha do define o nosso vetor em específico, ou seja, o seu sentido e sua magnitude.

Teríamos também , pois o campo elétrico se propaga ao longo do eixo (o que pode ser visto pelo argumento do coseno, que depende apenas de ) e ambos campo elétrico e campo magnético são perpendiculares à direção de propagação.

Se fizermos , teríamos . Assim, a resposta correta é a letra .

Passo 3

O método anterior tem um problema: Se fizéssemos , acharíamos também a letra como sendo correta. Então por que escolher a letra ?

Bem, como a questão pergunta a direção de polarização, esse raciocínio estaria correto. Porém, apenas a letra tem a direção e o sentido corretos do campo elétrico.

O segundo método de fazer que nos diz isso diretamente é o seguinte: Para a onda eletromagnética, temos que:

Ou seja, o produto vetorial entre a o sentido do campo elétrico e do campo magnético nos dão a direção e sentido de propagação da onda. Visualmente, temos:

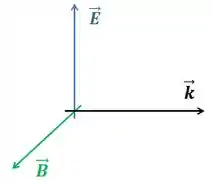
Da figura, temos então que:

Logo, podemos achar a direção do campo elétrico por um produto vetorial. Como queremos apenas a direção e sentido, vamos usar a direção e sentido do campo magnético.