Uma “cavidade linear” no vácuo é definida por duas paredes planas, paralelas e de material condutor ideal situadas em planos paralelos a e posicionados em e , respectivamente. Sabendo que uma onda eletromagnética é excitada dentro da cavidade no primeiro modo normal de oscilação, o campo elétrico dessa onda pode ser dado por:
a) .
b) .
c) .
d) .
Passo 1
Eai galerinha, bora resolver mais um problema de física 4 da UFRJ?
Nesse problema temos uma onda estacionária presa na região . Além disso, como as paredes que delimitam essa região são condutoras, os campos elétricos devem se anular em e em . Nas alternativas A, B e C isso ocorre pois
Já na alternativa D isso não acontece, pois para :
Com isso, já podemos descartar essa última alternativa...
Passo 2
Além disso, o campo elétrico deve ser perpendicular à direção em que a onda estacionária está localizada. Com isso, podemos descartar também a alternativa C, pois nela o campo está na direção .
Passo 3
Temos agora duas possibilidades: A ou B, eai, o que fazer?
Bom, o enunciado disse que a onda deve estar no primeiro modo normal de vibração. Vamos lembrar o que é isso:
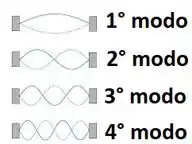
No primeiro modo de vibração, a onda não deve possuir nenhum nó. Lembre-se que o nó é um ponto em que a amplitude da onda é sempre nula. Para olhar para os nós das ondas, temos que analisar os termos:
No caso da alternativa A, os nós acontecem se
Para temos e para temos . Logo, nenhum ponto entre é nó para essa onda: isso significa que ela está no primeiro modo de vibração!
Já para a alternativa B, temos
Para temos e para temos , que representa os extremos da onda, até aqui tudo bem. Porém para , achamos . Isso significa que no meio da onda temos um nó: trata-se do segundo modo de vibração.
Como o enunciado pede o primeiro modo, devemos assinalar a alternativa A!
Resposta
Alternativa A.