Uma onda plana eletromagnética linearmente polarizada, propagando-se no vácuo no sentido positivo do eixo z, tem comprimento de onda e intensidade .
Parte dessa onda eletromagnética entra em uma placa transparente, de espessura (ver figura), tal que a velocidade de propagação se reduz a , incidindo com um ângulo de 30o em relação à normal da superfície da placa.
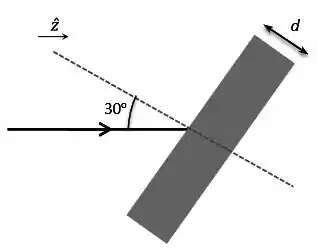
(d) Se no percurso dentro da placa a onda ganha uma fase de π, qual é a espessura da placa?
Passo 1
Nesse tipo de questão temos que lembrar de alguns conceitos bem importantes.
O primeiro é que, como no percurso a onda ganhou uma fase de π, significa que a distancia percorrida pela onda dentro do material foi de , isso significa que a diferença de fase entre a onda que entrou e a que saiu foi de metade do comprimento de onda no material, ou seja, a que calculamos no item C.
Com isso já sabemos de antemão que
Passo 2
Agora o que precisamos ver é como isso aparece na nossa peça, olhando a figura abaixo podemos ver bem o que ocorre
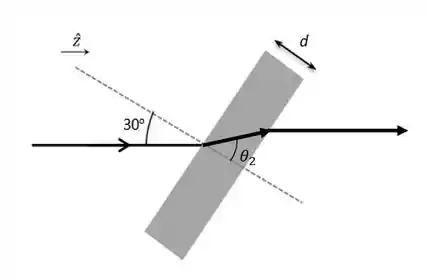
olhando o triangulo formado temos que
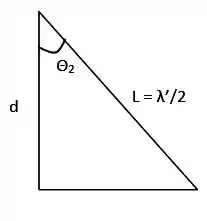
Dessa forma, podemos relacionar a distância percorrida pela nossa onda com a espessura da nossa peça, dessa forma teremos que
Com isso teremos que
Então vemos como é de suam importância determinarmos o ângulo
Passo 3
Olhando novamente a nossa figura vemos que podemos usar a lei de Snell
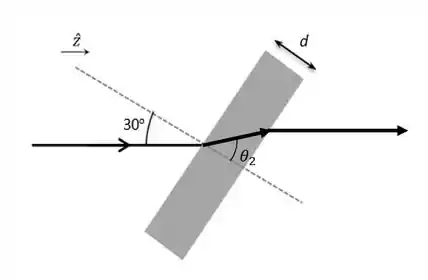
Em que
O valor do índice de refração do meio é uma relação entre a velocidade da luz no vácuo e a velocidade da luz no meio dada por
Substituindo na nossa fórmula teremos que
Passo 4
Agora que temos o valor do ângulo, basta que façamos o cálculo da espessura da nossa peça
Lembrando que
Substituindo na nossa fórmula teremos que