Um raio de luz monocromático parte do ar () e incide em uma face horizontal de um prisma triangular, conforme a figura com . O prisma possui o índice de refração igual a . Determine o valor do ângulo de incidência do raio da figura para que a reflexão na face inclinada do prisma seja com o ângulo crítico.
- .
- .
Passo 1
Para resolvermos essa questão, vamos dar uma olhada para a figura abaixo, em que a gente desenhou os raios incidentes, refratados e também as normais, além dos ângulos , que é o que precisamos encontrar, o ângulo de refração dentro do prisma e o ângulo para o qual ocorre a reflexão interna total.
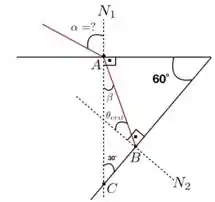
Precisamos, primeiro, encontrar qual é o valor desse ângulo crítico. Para isso, usamos a lei de Snell
Portanto, .
Passo 2
Agora, olhando para a figura e os triângulos dela, vemos que . Portanto, usando de novo a lei de Snell, podemos encontrar o ângulo :
Resposta
Letra d).