Você olha para baixo, em direção a uma moeda que está no fundo de uma piscina de profundidade e índice de refração .
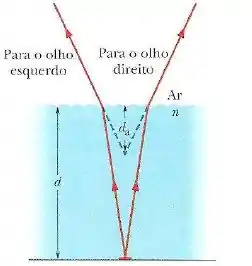
Como você observa a moeda com dois olhos, que interceptam raios luminosos diferentes provenientes da moeda, tem a impressão de que a moeda se encontra no lugar onda os prolongamentos dos raios interceptados se cruzam, a uma profundidade .
Supondo que os raios da figura acima não se desviam muito da vertical, mostre que .
(Sugestão: Use a aproximação, válida para ângulos pequenos, de que .)
Passo 1
Vamos começar fazendo uma análise gráfica do problema, mas para isso teremos que definir algumas coisas.
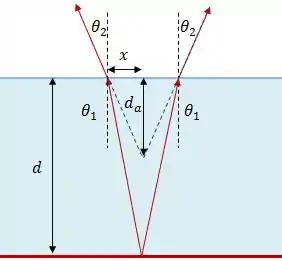
Na figura acima, e são os ângulos formados com a normal pelos raios incidentes e refratados, respectivamente. Além disso, é a distância entre o ponto em que os raios cruzam a interface entre os dois meios e o eixo central de onde se encontra a moeda.
Daqui podemos separar dois triângulos:
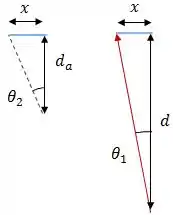
As tangentes de e são, respectivamente:
Considerando e suficientemente pequenos, podemos dizer que:
Passo 2
De acordo com a Lei de Snell, temos que:
Onde e, de acordo com o enunciado, , logo:
Fazendo as substituições das expressões que encontramos no Passo 1, teremos:
Organizando os termos, teremos, finalmente:
Resposta
Ei, a resposta está no passo a passo :)