Calcule o determinante:
Passo 1
Opa meus lindos, tudo bem com vocês? Bora lá resolver essa questão! A grande questão aqui é:
Como calcular o determinante de uma matriz ?
Você estão lembrados? Relaxa que eu te mostro!

Passo 2
O método mais tranquilinho pra gente poder calcular o determinante pra essa questão vai ser através do produto de alguns elementos da matriz. Para isso precisamos “copiar” as duas primeiras colunas ao lado da matriz, e depois multiplicar seguindo as diagoanais.
Fiz aqui um modelo visual pra gente poder visualizar melhor.
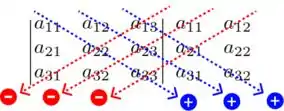
Lembrando que esses elementos da imagem, correspondem aos elementos de qualquer matriz . Traduzindo:
Elemento que se encontra na linha (horizontal) e na coluna (vertical) . Por exemplo, pra nossa matriz:
O elemento é aquele que se encontra na primeira linha e primeira coluna, logo o elemento:
Agora a vez de vocês: quem seria o elemento ? Seria o elemento na segunda linha e terceira coluna, logo:
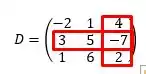
O elemento é o . E por aí vai.
Passo 3
Belezinha, temos então a nossa matriz:
Aplicando a primeira parte do método, que é replicar as duas primeiras colunas ao lado da matriz:
Belezura. Agora vem a parte mais legal! Sabe o método? Esse:
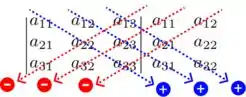
Então, vamos seguir as setas em azul realizando o produto dos elementos na mesma seta, e SOMANDO com a o produto da próxima seta e por aí vai. Para as setas em vermelho, vamos realizar o produto dos elementos na mesma seta e SUBTRAIR. Ou seja, o determinante da matriz vai ser calculado por:
Bora jogar na matriz da nossa questão? Simbora! Temos então que para:
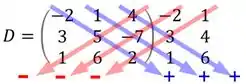
O determinante pode ser calculado como:
Calculando:
E aqui encontramos o determinante! E é isso gente boa! Se ficou alguma dúvida, quer dar alguma sugestão ou reportar algum erro, manda um feedback pra gente! Vamos adorar ajudar você