UNB – Sem campus - Introdução a Álgebra Linear – Listas – Listas de IAL UnB – Lista 2 – 2f
Calcule o determinante:
Passo 1
Opa meus lindos, tudo bem com vocês? Bora lá resolver essa questão! Aqui somos apresentados pra matriz:
E a partir daqui calcular o determinante! Ela é meio diferente com umas variáveis no meio mas sem problemas, a questão só quer tentar complicar as coisas. Você lembra como calculamos o determinante?
Passo 2
Existem muitas maneiras de calcular determinantes. Pra nossa matriz, a maneira mais eficiente vai ser através do produto de alguns elementos da matriz, quando a gente “copia” as duas primeiras colunas ao lado da matriz. Fiz aqui um modelo visual pra gente poder visualizar melhor.
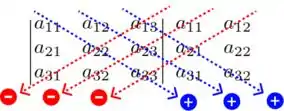
Lembrando que esses elementos da imagem, correspondem aos elementos de qualquer matriz 3X3. Traduzindo:
Elemento que se encontra na linha (horizontal) e na coluna (vertical) . Por exemplo, pra nossa matriz:
O elemento é aquele que se encontra na segunda linha e segunda coluna, logo o elemento:
Agora a vez de vocês: quem seria o elemento ? Seria o elemento na primeira linha e segunda coluna, logo:
O elemento é o . E por aí vai.
Passo 3
Belezinha, temos então a nossa matriz:
Aplicando a primeira parte do método, que é replicar as duas primeiras colunas ao lado da matriz:
Belezura. Agora vem a parte mais legal! Sabe o método? Esse:
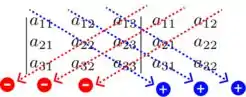
Então, vamos seguir as setas em azul realizando o produto dos elementos na mesma seta, e SOMANDO com a o produto da próxima seta e por aí vai. Para as setas em vermelho, vamos realizar o produto dos elementos na mesma seta e SUBTRAIR. Ou seja, o determinante da matriz vai ser calculado por:
Bora jogar na matriz da nossa questão? Simbora! Temos então que para:
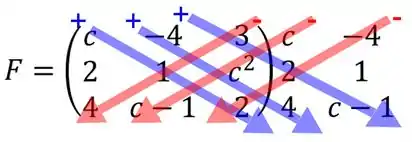
O determinante pode ser calculado como:
Calculando:
Desenvolvendo e organizando por expoente:
E aqui encontramos o determinante! E é isso gente boa! Se ficou alguma dúvida, quer dar alguma sugestão ou reportar algum erro, manda um feedback pra gente! Vamos adorar ajudar você