Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Regra dos Trapézios

Ver Teoria
Exercício 91234567810

Enunciado

Universidade Federal de Pernambuco, Área II, Cálculo Numérico, 2019-2, 2ª prova, 15/10/2019, 3.

3. Determine o menor número de intervalos cujo erro no cálculo da integral abaixo pelo método dos trapézios seja menor que 1 0 - 6 . Utilize 3 casas decimais e arredondamento padrão.

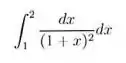
Passo 1

Oiii, pessoal! Tudo bom? Nesta questão vamos ver mais um pouco sobre um dos métodos de integração, o método dos trapézios! Ele é muito útil para nos ajudar a aproximar aquelas integrais hiper mega ultra difíceis de resolver hahahaha

Mas a gente sabe que toda aproximação tem um erro associado, né? E às vezes é muito importante definir esse erro ou tentar limitá-lo. No caso do método dos trapézios, o módulo do erro E T segue esta equação:

| E T | = h 3 ⋅ n 12 ⋅ m a x x ϵ [ a , b ] | f ' ' ( x ) | ,   h = b - a n

Sendo que n é o número de intervalos, [ a , b ] o intervalo de integração e f ' ' ( x ) a segunda derivada da função.

Passo 2

Vamos então calcular as duas primeiras derivadas de f ( x ) = 1 ( 1 + x ) 2 . Nesse caso precisamos usar a regra do quociente, da cadeia e do tombo. Tranquilo!

f ' ( x ) = [ 1 ] ' ⋅ [ ( 1 + x ) 2 ] - [ ( 1 + x ) 2 ] ' ⋅ 1 [ ( 1 + x ) 2 ] 2 = - 2 ( 1 + x ) ( 1 + x ) 4 = - 2 ( 1 + x ) 3

f ' ' ( x ) = [ - 2 ] ' ⋅ [ ( 1 + x ) 3 ] - [ ( 1 + x ) 3 ] ' ⋅ - 2 [ ( 1 + x ) 3 ] 2 = - 6 ( 1 + x ) 2 ( 1 + x ) 6 = - 6 ( 1 + x ) 4

Devemos verificar agora para qual valor de x do intervalo de integração ( a = 1 ou b = 2 ) temos o valor máximo do módulo de f ' ' ( x ) :

| f ' ' ( a ) | = 6 ( 1 + 1 ) 4 = 0,375 e | f ' ' ( b ) | = 6 ( 1 + 2 ) 4 = 0,07

Passo 3

Show, galera! Vamos agora substituir todas essas informações na fórmula do erro.

| E T | = ( b - a n ) 3 ⋅ n 12 ⋅ m a x x ϵ [ a , b ] | f ' ' ( x ) | = ( 2 - 1 ) 3 ⋅ n 12 ⋅ n 3 ⋅ 0,375 = 0,03125 n 2

Como queremos o menor número de intervalos cujo erro seja menor que 1 0 - 6 , devemos ter:

| E T | = 0,03125 n 2 < 1 0 - 6   ↔ n > 0,03125 ⋅ 1 0 6 = 176,777

Mas n é um número inteiro, galera! E o número inteiro mais próximo de 176,777 é 177 ! Beleza?

Resposta

Devemos ter pelo menos 177 intervalos para que o erro no cálculo da integral seja menor que 1 0 - 6 .

Exercícios de Livros Relacionados

Qual o erro máximo cometido na aproximação de ∫ 0 4 ( 3 x 3 - 3 x + 1 ) d x pela regra dos Trapézios com quatro subintervalos?
Calcule as integrais a seguir pela regra dos Trapézios usando quatro e seis divisões de [a,b]. ∫ 1 2 e x d x ∫ 1 4 x d x ∫ 2 14 d x x
Em que sentido a regra de Simpson é melhor do que a regra dos Trapézios?
Usando as integrais do exercício anterior com quantas divisões do intervalo, no mínimo, podemos esperar obter erros menores que 1 0 - 5 ?
11. a) Comprove gráfica e analiticamente que se:i) f ' ' ( x ) é contínua em [ a , b ] , eii) f ' ' x0 , ∀ x ∈ [ a , b ] ,então, a aproximação obtida para ∫ a b f x d x pela regra dos Trapézios é maio