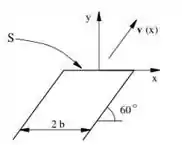
Calcule a taxa volumétrica e mássica, e , respectivamente, através da superfície de largura mostrada na figura, onde o vetor velocidade faz um ângulo de 60˚ com o eixo x e sua magnitude é dada por . A densidade do fluido é .
Passo 1
Bom, a gente já sabe que a taxa volumétrica é dada pela expressão:
Onde esse produto é escalar, logo ele é calculado pela multiplicação do módulo dos vetores vezes o cosseno do ângulo formado entre eles: , beleza?
A gente já tem a expressão da velocidade, falta a gente saber que ângulo usar!O problema disse que a velocidade faz um ângulo de 60˚ com o eixo x, mas o vetor normal da superfície S é paralelo ao eixo y, logo o ângulo que a gente vai usar é 30˚!
Então bora resolver a nossa integral!
Passo 2
Como estamos integrando a área, e ela tem duas dimensões, vamos fazer uma integral dupla variando de 0 a em x, e de 0 a em z (que seria o eixo entrando na tela)!
Lembrando que o vetor normal é unitário, então o módulo dele é 1!
Integrando essa expressão em relação a x temos:
Aplicando os limites de integração:
Integrando em relação à z:
Finalmente:
Passo 3
Agora calculando a taxa mássica:
Considerando a densidade constande, ela pode ser reescrita como:
Assim: