Na condensação em fime em uma placa vertical em uma atmosfera de vapor, Nussel descobriu que quando o escoamento é laminar, o perfil de velocidade em x é:
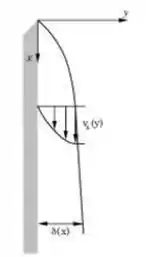
Onde e são as densidades do fluido nas fases líquido e vapor, respectivamente, e a viscosidade do fluido. Encontre o taxa volumétrica por unidade de comprimento em qualquer valor de .
Passo 1
Bom, a gente já sabe que a taxa volumétrica é dada pela expressão:
Felizmente ele já deu o perfil de velocidade! Como o problema quer a taxa por unidade de comprimento (já que não sabemos a profundidade da placa), então a gente só precisa integrar em relação à y :D
Passo 2
Substituindo então a expressão da velocidade:
A primeira parte é toda constante então a gente pode colocar ela pra fora:
Integrando em relação à y:
Aplicando os limites de integração: