A barra abaixo foi sujeita ao carregamento mostrado.
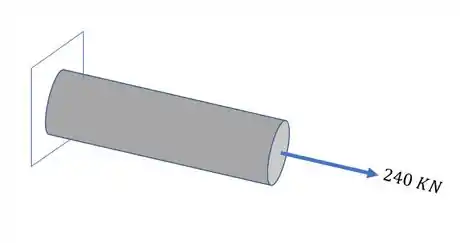
Sabendo que o raio da peça é de 30 mm e que o fator de segurança usado para essa peça para a tensão Normal foi de 1,47 e que para a tensão Cisalhante foi de 2,11 no pior caso de carregamento possível, determine os valores de e
Passo 1
Nessa questão sabemos que devemos determinar o valor das tensões admissíveis, para isso vemos na fórmula abaixo que precisamos do valor do fator de segurança que é dado no enunciado e do valor das tensões máximas tanto cisalhante quanto normal, que já veremos como determinar. Sabemos que
Ou
Que nos fornece o fator de segurança para cada tensão
Também sabemos que devemos determinar o estado de tensões da nossa peça, e com base nesse estado de tensões faremos
Que nos fornece a média das tensões
Que nos da o cisalhante máximo que o nosso elemento foi submetido
A última fórmula é dada por
Que de fato nos fornece o valor das tensões principais que serão usadas no nosso fator de segurança.
Passo 2
Olhando a nossa figura sabemos que devemos fazer primeiro um elemento infinitesimal na nossa peça, como mostra a figura
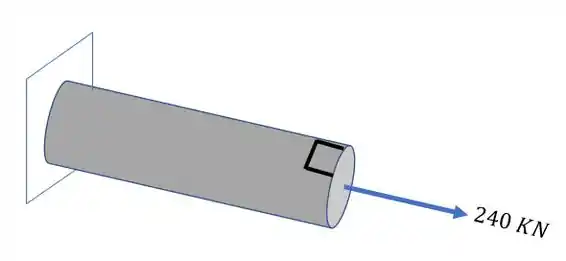
Sabemos que o que estará agindo no nosso elemento é um esforço de tração dado pela fórmula
Sabemos que
Substituindo teremos que
Olhando o nosso elemento infinitesimal, teremos que
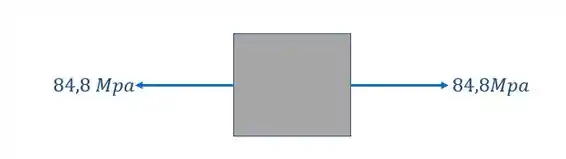
Assim como temos as fórmulas, também temos os dados necessários para resolver a questão, que são dados por
Vamos resolvendo agora cada fórmula passo a passo
Passo 3
Agora que já sabemos os dados, vamos determinar os valores necessários para encontrarmos os valores das tensões principais.
Sabemos que
Então
Também sabemos que
Logo
Passo 4
Como já temos esses valores, podemos facilmente determinar os valores das tensões máximas pelas fórmulas
Substituindo
O cisalhante máximo é muito simples, é o próprio valor do R que já calculamos
Passo 5
Sabemos que para determinarmos o fator de segurança devemos fazer a divisão entre a maior tensão suportada pela peça e a maior tensão aplicada a peça, dessa forma temos a fórmula
Ou
Sabemos que
E com relação as tensões máximas teremos que
Substituindo teremos que
Fazendo isso teremos que