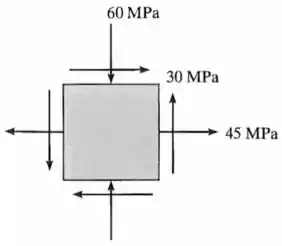
O estado de tensão em um ponto é mostrado no elemento. Determine as tensões principais e a tensão de cisalhamento máxima no plano e a tensão normal média no ponto. Especifique a orientação do elemento em cada caso.
Passo 1
O que está acontecendo?
O exercício nos fornece um estado plano de tensões em que:
Lembrando que tem um valor negativo nesse caso pois a sua direção no desenho está no sentido oposto ao da convenção, a convenção de sinais é a seguinte:
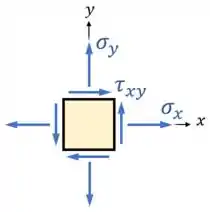
Observe que as tensões normais são trativas e a tensão cisalhante tem aquela direção apontada no desenho. Isso significa que a tensão fornecida é compressiva!
E o que é que o exercício quer?
No item , ele quer saber as tensões principais e e as orientações e correspondentes.
E no item b?
Já no item , o exercício quer saber a tensão de cisalhamento máxima nesse elemento, além da tensão normal média e da orientação correspondente.
Para tanto, podemos aproveitar que já calculamos e durante a resolução do item anterior.
Enquanto que uma ou mais orientações podem ser obtidas somando OU subtraindo de ou .
Passo 2
Depois de já termos definido o estado plano de tensões no passo anterior:
Já estamos prontos para iniciar a determinação das tensões principais para o item !
Começamos calculando :
E :
Em seguida, já calculamos e :
Passo 3
Agora, para complementar a resposta do item , precisamos determinar as orientações e .
Começamos aplicando:
Aí, utilizando a função da calculadora, encontramos:
O que significa que:
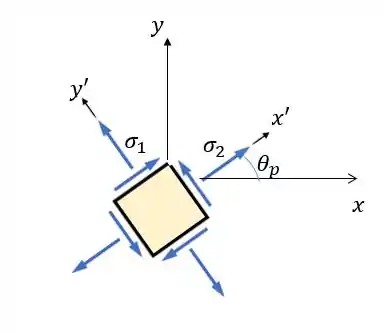
Pessoal, a gente pode visualizar as tensões e juntamente com o ângulo no nosso estado plano de tensões:
Passo 4
Agora, precisamos testar esse valor de para descobrirmos qual é a tensão principal que ele causa.
Para tanto, empregamos a fórmula da transformação de tensões para :
Substituindo todos os valores, temos:
O que dá:
O que é igual à .
Dessa forma, concluímos que é na realidade o ângulo :
E o ângulo ?
Podemos encontrar ele somando ou subtraindo de .
Normalmente, evitamos encontrar ângulos fora do intervalo , então vamos subtrair de para encontrarmos que:
E pronto!
Resolvemos o item por completo.
Passo 5
Em seguida, para o item , podemos aproveitar os valores “” e “” que já calculamos para o item , conforme vimos lá no passo 1.
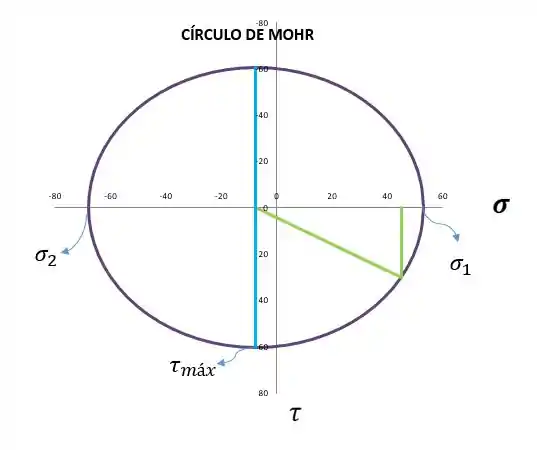
Para saber a tensão de cisalhamento máxima , podemos aproveitar que para encontrarmos que:
Enquanto que para , podemos aproveitar diretamente o valor que já calculamos lá no passo 2 :
Por fim, para encontramos orientações em que essa tensões e ocorrem, podemos somar OU subtrair de OU .
Evitando encontrar ângulos fora do intervalo , encontramos dessa forma que:
E assim completamos nossa resposta para o item !