Um porto sofre na ancoragem de navios esforços solicitantes que podem causar o seu colapso, principalmente quando ocorre encontro de grandes navios com a estrutura do porto. Em um dia foi constatado que a ancoragem de um navio exerceria sobre um porto uma força de 1000000 MN de força em uma área de 20 . Considere os seguintes dados.
A tensão cisalhante ao qual um elemento infinitesimal do material usado no porto é de 500Gpa. A estrutura do porto é extremamente forte para qualquer ação cisalhante, mas pode romper pela ação de um esforço normal que supere 600Gpa para o caso de compressão, ou 400GPa para o caso de tração. E não são considerados esforços na direção y do elemento infinitesimal.
Sabendo disso determine se o porto resistiria aos esforços provocados pela atracação desse navio.
Passo 1
Aqui vale perceber como ele apresenta alguns termos que já conhecemos.
Primeiro ele fala de uma força aplicada em uma determinada área do porto, como visualmente entendemos como se fosse uma pancada da lateral do navio com o porto, entendemos que essa solicitação se trata de um esforço normal de compressão, colocando em termo que conhecemos podemos escrever como
Como ele diz que esse esforço irá atuar sobre uma área de , podemos determinar, dessa maneira, a tensão normal no nosso porto, usando a fórmula
Passo 2
Também vale ressaltar o que ele diz sobre outros esforços. Ele afirma que não consideraremos tensões na direção y, logo
Também é dito no enunciado que a ação cisalhante no momento do impacto é de 500GPa, em termos que conhecemos
Por fim nos é dito que o porto pode suportar qualquer ação cisalhante (logo não precisamos nos preocupar com o cisalhante máximo) porém, para uma ação de 600GPa do esforço normal o nosso porto romperia por compressão, ou ainda a um esforço de tração ele romperia quando chegasse em 400GPa, com isso ele nos mostra que
Agora que já temos tudo que precisamos, vamos montar o nosso elemento infinitesimal.
Passo 3
Nosso elemento ficará
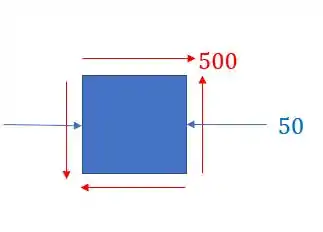
Como já sabemos, nesse estado o nosso elemento não está rompendo, pois já sabemos que o rompimento ocorre quando a tensão normal ultrapassa 600GPa, mas será que alguma tensão principal pode romper o nosso elemento? Vamos testar.
Passo 4
Nessa questão sabemos que devemos determinar o valor das tensões principais.
Sabemos pela teoria quais fórmulas nos auxiliam nisso, sendo essas fórmulas dadas por
Que nos fornece o plano em que as tensões principais ocorrem
Que nos fornece a média das tensões
Que nós dá o cisalhante máximo que o nosso elemento foi submetido
A última fórmula é dada por
Que de fato nos fornece o valor das tensões principais
Passo 5
Assim como temos as fórmulas, também temos os dados necessários para resolver a questão, que são dados por
Vamos resolvendo agora cada fórmula passo a passo
Primeiro vamos determinar a orientação em que ocorre as tensões principais
Isso é uma das orientações dos planos, mas também pode-se encontrar o outro subtraindo 90° do que encontramos
Passo 6
Agora que já sabemos qual é a orientação do plano, vamos determinar os valores necessários para encontrarmos os valores das tensões principais.
Sabemos que
Então
Também sabemos que
Logo
Passo 7
Como já temos esses valores, podemos facilmente determinar os valores das tensões máximas pelas fórmulas
Substituindo
O cisalhante máximo é muito simples, é o próprio valor do R que já calculamos
Passo 8
Agora precisamos pegar as nossas tensões principais e avaliar
Primeiro vamos analisar a compressão
Sabemos que na compressão a tensão admissível é de 600GPa, ou seja, quando comparamos com a nossa tensão principal de compressão, sabemos que o porto suportara a atracação desse navio.
Segundo vamos analisar a tração
Sabemos que na tração a tensão admissível é de 400GPa, ou seja, quando comparamos com a nossa tensão principal de tração, sabemos que o porto não suportara a movimentação do navio, tendo que tomar os devidos cuidados para que a atracação do navio não destrua o porto.
Mas já que sabemos que rompe na tração, em que sentido será esse rompimento?
Passo 9
Passo 10
Passo 11
Agora precisamos usar a fórmula
Substituiremos os nossos valores dado no elemento e escolheremos um dos ângulos para testar, assim saberemos a qual tensão cada ângulo pertence
Fazendo
Teremos que
Logo vemos que o ângulo que chamamos de 2 pertence a tensão 1, apenas para que fique homogêneo faremos que
E
Se já descobrimos a quem pertence um dos ângulos, com certeza o outro pertence a outa tensão.
Resposta
O porto não suportara pois rompera pelos esforços de tração que ocorrem na orientação de 46,43°