Uma força cisalhante age sobre uma área retangular de um foquete de 15 x 25m(área de ação da força). sabendo que a máxima tensão cisalhante suportada pelo foguete é de 50Mpa, e que a força aplicada é de 15000MN, determine se a estrutura dessa foguete resistiria a ação dessa força. Desprezar atuação de esforços normais na direção y e considere esforços normais na direção x de 30 Mpa. Também vale ressaltar que o foguete apresenta alta resistência a esforços normais.
Passo 1
Aqui vale perceber como ele apresenta alguns termos que já conhecemos.
Primeiro ele fala de uma força aplicada em uma determinada área do foguete, como essa força age lateralmente, sabemos que se trata de um esforço cortante.
Como ele diz que esse esforço irá atuar sobre uma área de , podemos determinar, dessa maneira, a tensão cisalhante no nosso foguete, usando a fórmula
Passo 2
Também vale ressaltar o que ele diz sobre outros esforços. Ele afirma que não consideraremos tensões na direção y, logo
Também é dito no enunciado que a ação normal no momento do impacto é de 30Mpa na direção x, em termos que conhecemos
Por fim nos é dito eu o foguete suporta 50Mpa de esforço cisalhante e possui altíssima resistência com relação a esfroços normais, ou seja, devemos nos preocupar com o valor do cisalhante máximo.
Agora que já temos tudo que precisamos, vamos montar o nosso elemento infinitesimal.
Passo 3
Passo 4
Nosso elemento infinitesimal será dado por
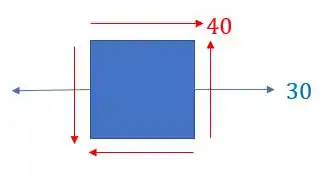
Como já sabemos, nesse estado o nosso elemento não está rompendo, pois já sabemos que o rompimento ocorre quando a tensão cisalhante ultrapassa 50MPa, mas será que o cislahante máximo ultrapassa esse valor?
Passo 5
Vamos diret ao que interessa, sabemos que o nosso cisalhante máximo é dado pelo valor de R, e sabemos que a fórmula que nos da R é
Substituindo os nossos dados temos que
Vemos então que o cisalhante máximo não ultrapassa o valor da tensão cisalahnte admissível.
Nesse caso, como sabemos que o material não rompe, não existe a necessidade de calcular a orientação do elemento, já que ele não representaria nada mais que uma rientação para o cisalhante máximo.
É importante lembrar que também não calculamos as tensões principais pelo fato de o material do foguete ser altamente resistente a tensões normais.
Resposta
O foguete resiste a ação da tensão cisalhante agindo nele já que máximo cislahante alcançado é de 42,72 Mpa quando a resistência máxima é de 50Mpa.