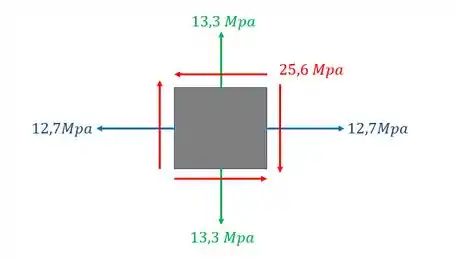
Um tubo de aço de paredes finas sofre a ação de um liquido pressurizado nas suas paredes internas. Sabendo que na pior situação de carregamento possível o elemento infinitesimal é o dado abaixo, determine se haverá segurança para a peça, ou seja, se os fatores de segurança para o normal e para o cisalhante na pior situação suportaram o carregamento dado.
Passo 1
Nessa questão sabemos que devemos determinar o valor das tensões principais, assim como o valor do cisalhante máximo, pois ambos nos ajudaram no cálculo do fator de segurança
Sabemos pela teoria quais fórmulas nos auxiliam nisso, sendo essas fórmulas dadas por
Ou
Que nos fornece o fator de segurança para cada tensão
Que nos fornece a média das tensões
Que nos da o cisalhante máximo que o nosso elemento foi submetido
A última fórmula é dada por
Que de fato nos fornece o valor das tensões principais que serão usadas no nosso fator de segurança.
Passo 2
Assim como temos as fórmulas, também temos os dados necessários para resolver a questão, que são dados por
Vamos resolvendo agora cada fórmula passo a passo
Passo 3
Agora que já sabemos os dados, vamos determinar os valores necessários para encontrarmos os valores das tensões principais.
Sabemos que
Então
Também sabemos que
Logo
Passo 4
Como já temos esses valores, podemos facilmente determinar os valores das tensões máximas pelas fórmulas
Substituindo
O cisalhante máximo é muito simples, é o próprio valor do R que já calculamos
Passo 5
Sabemos que para determinarmos o fator de segurança devemos fazer a divisão entre a maior tensão suportada pela peça e a maior tensão aplicada a peça, dessa forma temos a fórmula
Ou
Sabemos que
E com relação as tensões máximas teremos que
Calculando os fatores de segurança, teremos
Aqui vale ressaltar um ponto muito importante, a nossa peça não possui fator de segurança, pois ela rompe com o carregamento que estamos usando. Mas como percebemos isso?
Sempre que o nosso fator de segurança der menor que 1 significa que a nossa peça sofreu um rompimento, isso ocorre pois significa que a tensão máxima aplicada é maior que a tensão máxima admissível, logo ocorre o rompimento e independente do fator de segurança que usemos para o cisalhante a peça romperá pelo esforço normal.
Resposta
A nossa peça não possui fator de segurança pois ela rompe antes, isso se deve ao fato de termos calculado que
Ou seja, a tensão máxima suportada pela nossa peça é 35 Mpa, mas o que está aplicado nela é 38,6, ou seja, mesmo que o cisalhante suporte as tensões aplicadas nela, o normal não suportará, levando a peça ao rompimento.