O tubo de aço tem de diâmetro externo e uma espessura de parede de . Sabendo que o braço está rigidamente fixado ao tubo, determine as tensões principais e a tensão de cisalhamento máxima no ponto .
Passo 1
O que está acontecendo?
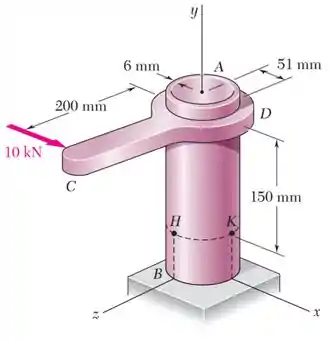
O tubo tem:
- Um diâmetro externo e consequentemente um raio externo ;
- E uma parede de espessura , e consequentemente um raio interno .
A força de é aplicada no braço , resultando no aparecimento de vários esforços internos ao longo do tubo .
E o que é que o exercício quer?
Ele quer saber as tensões principais e e a tensão máxima de cisalhamento no ponto .
Daí que, para encontramos isso, vamos ter que:
1. Realizar uma análise dos esforços internos na seção em que se encontram os pontos e , com o objetivo de descrever os esforços internos nessa seção.
2. Para cada um dos esforços internos encontrados no passo anterior, calcular e verificar o sentido da tensão causada por esses esforços interno.
3. Juntar os resultados dos passos anteriores para desenhar o estado plano de tensões para o ponto , definindo assim as tensões , e nele.
E finalmente, 4. Calcular e utilizando as fórmulas:
Para depois determinarmos as tensões principais , e a tensão de cisalhamento máxima nesse ponto!
Passo 2
Então vamos começar pela análise dos esforços internos.
Precisamos secionar o tubo na seção em que se encontram os pontos e .
Fazendo o uso de um desenho simplificado do conjunto e fazendo essa seção, vamos ter:
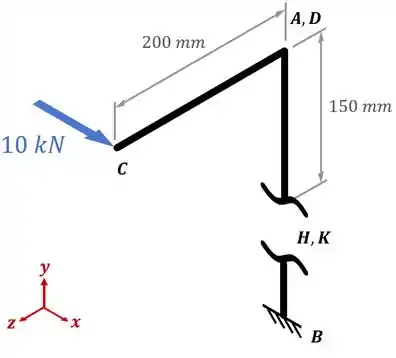
Aí, agora, temos que nos lembrar dos possíveis esforços internos que podem existir nessa seção:
- Força Normal ;
- Força Cortante , que para essa seção em um conjunto em como esse, pode existir tanto ao longo do eixo quanto ao longo do eixo ;
- Torque Interno , que também pode ser chamado de momento torsor ou de momento em volta do eixo , ;
- E momentos fletores ou , que para essa seção em um conjunto em como esse, pode existir tanto em volta do eixo quando em volta do eixo .
Mas aí...
Percebendo que a única força externa na nossa peça é a força de , percebemos que ela não vai gerar:
- Nenhuma força normal ;
- Nenhuma força cortante ao longo do eixo ;
- & nenhum momento fletor em volta do eixo .
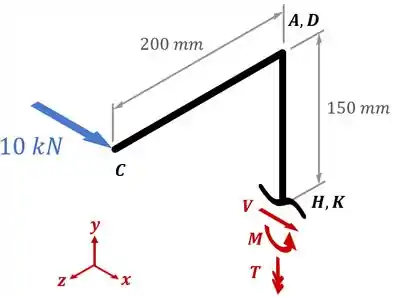
Então os nossos esforços internos na nossa seção vão ficar assim:
Passo 3
Agora, podemos aplicar o equilíbrio no desenho que fizemos no passo anterior para encontrarmos o valor de cada esforços interno.
Começando pelo equilíbrio de forças no eixo , temos:
O que significa que:
Seguindo com o equilíbrio de torques para o nosso tubo , temos:
Aí aqui, vamos ter dois torques no nosso tubo:
- o torque interno , que desenhamos de forma a estar no sentido oposto do eixo (sentido negativo);
- e o torque gerado pela força de com um braço de , que pela regra da mão direita vai estar no sentido do eixo (sentido positivo).
Dessa forma, o nosso somatório de torques fica assim:
O que significa que:
Ou, em :
Para finalizar, utilizamos o equilíbrio de momentos em relação ao ponto da seção:
Aqui, vamos ter o momento fletor no sentido anti-horário () e um momento gerado pela força de com um braço de no sentido horário ().
Então, nosso somatório fica assim:
Isolando , encontramos:
Ou, em :
Passo 4
Chegou a hora de calcular e avaliar o sentido de cada tensão causada por cada um desses esforços internos.
Começando pela força de cisalhamento :
Sabemos que a tensão de cisalhamento causada por uma força de cisalhamento é nula no topo e na base de uma seção.
E, nesse nosso caso, nós temos uma força de cisalhamento ao longo do eixo .
E, ao longo do eixo , o nosso ponto está efetivamente no topo da seção:
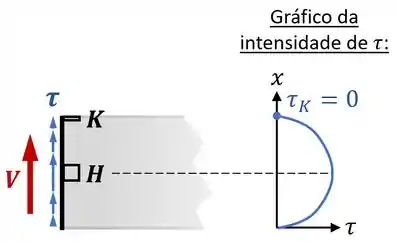
Então...
A tensão de cisalhamento devido a força de cisalhamento é nula no ponto .
Passo 5
Seguindo com o torque interno .
Pelo que estudamos lá em torção, sabemos que ele vai causar uma tensão de cisalhamento nos pontos da nossa seção de acordo com a fórmula:
Onde:
- é a distância entre o centro da seção e o ponto em que queremos avaliar a tensão (no nosso caso, o ponto , que está na superfície externa do tubo de tal forma que );
- & é o momento polar de inércia, que podemos calcular para um tubo vazado como:
Sendo que, substituindo e , isso dá:
Aí, aplicando a fórmula da torção para o nosso ponto , temos:
E substituindo , e , encontramos que:
Finalmente, calculando tudo e sabendo que é o mesmo que , encontramos que:
Passo 6
Agora, antes de seguir para a tensão causada pelo momento fletor , temos que entender o sentido dessa tensão causada pelo torque interno .
Para tanto, podemos olhar para a forma como desenhamos nosso torque interno lá no passo 2, mas dessa vez também olhando para o posicionamento de em relação à esse torque:
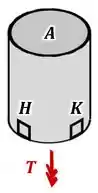
Aí, usando a regra da mão direita:

...conseguimos visualizar como é o sentido desse torque e da tensão causada por ele:
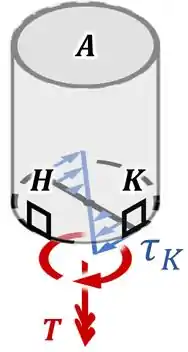
Assim, percebemos que o cisalhamento causado pelo torque no ponto aponta para a esquerda na aresta inferior do elemento :
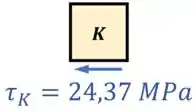
Mas aí, nós já estudamos também como um cisalhamento em uma aresta tem que ser equilibrado por cisalhamentos em outras arestas, de forma a não provocar um movimento do ponto .
Dessa forma, o cisalhamento no ponto fica assim:
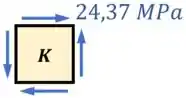
Passo 7
Por fim, chegamos a tensão causada pelo momento fletor .
Sabemos que um momento fletor causa em uma seção tensões normais de acordo com a fórmula da flexão:
Onde:
- é a posição do ponto em que se quer medir a tensão (nesse caso, o nosso ponto ) em relação à linha neutra/centróide da seção;
- & é o momento de inércia da área da seção, que para uma seção circular vazada é dado pela fórmula:
Dessa forma, substituindo e , vamos encontrar que:
Aí, na hora de aplicarmos a fórmula da flexão para o nosso ponto , podemos aplicá-la em módulo:
Isso porque, como estamos lidando com um problema 3D, a fórmula da flexão não é confiável para fornecer o sinal da tensão .
É mais seguro calcular a intensidade de e depois olhar com calma para a forma que desenhamos o momento para descobrirmos se ele causa tração ou compressão no ponto .
Então vamos lá!
Aplicando a fórmula da flexão para , temos:
Aí, substituindo:
- ;
- , uma vez que a linha neutra/centroide da nossa seção circular vazada está bem no meio da seção enquanto que o nosso ponto está na superfície externa da seção;
- & ,
Vamos ter que:
Finalmente, calculando tudo isso e sabendo que é o mesmo que , encontramos que:
Passo 8
Falta entendermos o sentido dessa tensão , então vamos olhar para a forma como desenhamos nosso momento fletor :
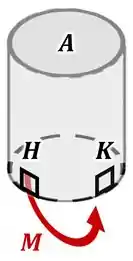
Olhando para essa figura, percebemos que o momento comprime o ponto ao longo da vertical (eixo ).
Dessa forma, temos que:
Sendo que o sinal de negativo indica que essa tensão é uma compressão.
Passo 9
Agora, podemos desenhar e definir o estado plano de tensões para o ponto .
Pegando o desenho que tínhamos feito no final do passo 6 e adicionando a compressão na vertical de , obtemos nosso estado plano de tensões para :
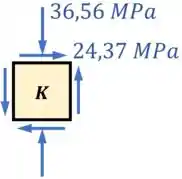
Aí, a partir desse desenho, conseguimos definir as nossas tensões , e para o ponto :
Passo 10
FINALMENTE, chegamos ao último passo desse exercício.
Chegou a hora de calcular as tensões principais e a tensão de cisalhamento máxima no ponto .
Para tanto, começamos calculando e :
E em seguida, aplicamos que:
Para encontrarmos nossas respostas: