Ache o volume do sólido gerado pela revolução da área sombreada por em torno do eixo .
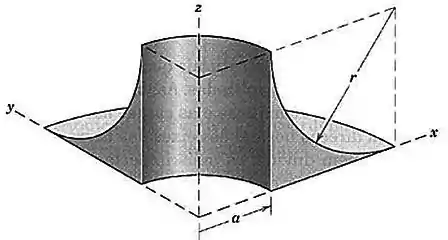
Passo 1
Para achar o volume temos que usar a seguinte equação:
O é a distância do centro da figura até o eixo (que é o eixo em torno do qual a figura gira). Porém, não sabemos onde está localizado o centro desta figura aqui:
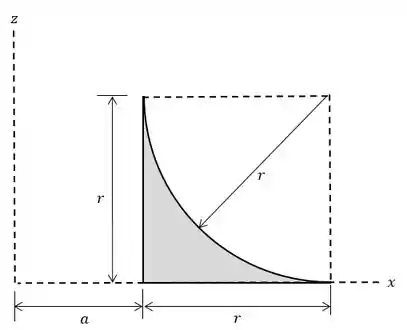
Mas perceba que a nossa figura é um quadrado do qual foi retirado um pedaço de círculo... Isso te lembra alguma coisa?
Se você pensou em corpos compostos acertou!!!
Passo 2
Então, vamos começar achando o centróide da nossa figura.
Para o quadrado, vamos ter a seguinte área:
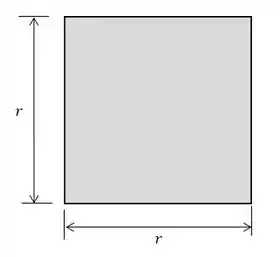
Já a área do pedaço correspondente a de círculo é:
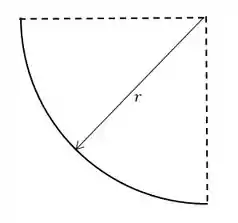
Não esqueça que a área do pedaço do círculo é negativa, pois estamos o retirando da área do quadrado.
Passo 3
Vamos achar a coordenada da centróide de cada uma das partes que compõe a nossa figura.
Para o quadrado vamos ter o seguinte:
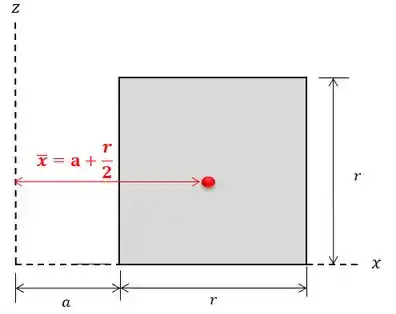
Antes de achar o centróide do pedaço correspondente a de círculo devemos saber que a posição do centróide fica assim:
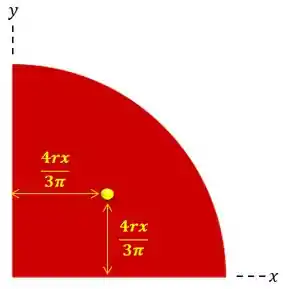
Então, o nosso pedaço de círculo fica assim:
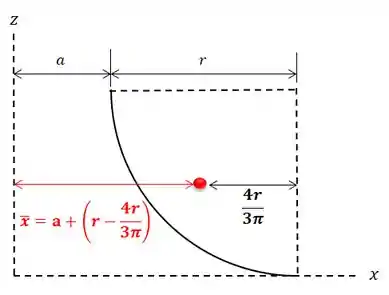
Passo 4
Vamos montar a tabela para facilitar nossos cálculos:

A área total será a soma das duas áreas:
Agora vamos multiplicar cada área por sua respectiva coordenada :
E:
Então, nossa tabela completa fica assim:

A soma das expressões que acabamos de achar é:
Então, a coordenada é:
Repare que a coordenada é justamente o nosso !!!
Passo 5
Agora temos que calcular o volume do sólido:
Repare que a coordenada é justamente o nosso :
E a área também já calculamos:
O ângulo corresponde a quanto a figura gira em torno do eixo e no nosso caso é , mas temos que passar isso para radianos. Vamos fazer uma regra de sabendo que corresponde a radianos:
Agora sim podemos calcular o volume:
Podemos ajeitar mais ainda esta equação: