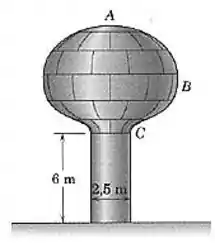
O tanque de armazenamento de água é uma casca de revolução e deve ser recoberto com duas camadas de tinta, que dá uma cobertura de por galão. O engenheiro (que se lembra de mecânica) consulta um desenho em escala do tanque e determina que a linha curva tem um comprimento de e que seu centróide está a da linha do centro do tanque. Quantos galões de tinta serão usados para o tanque, incluindo a coluna cilíndrica vertical?
Passo 1
Temos duas áreas: a do cilindro e a da esfera:
Para achar a área da superfície de um cilindro temos que usar a seguinte fórmula:
Onde é a altura do cilindro e é o raio.
Repare que o nosso cilindro é:
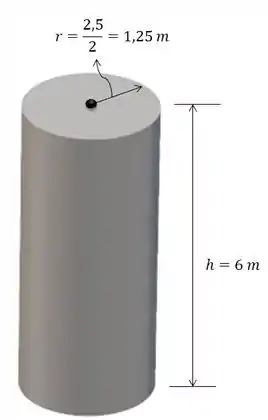
Então, a área superficial do nosso cilindro é:
Passo 2
Já para a esfera, vamos usar a nossa fórmula:
Já foi dito no enunciado que o centróide da curva é de , então:
E o perímetro também foi dado no enunciado e vale:
Com esses dados, podemos calcular a área da superfície da esfera:
Passo 3
Agora vamos calcular a área total:
Passo 4
Foi dito no enunciado que um galão cobre , então vamos fazer uma regra de três para achar o número de galões necessário para cobrir esta área que calculamos:
Então:
Mas repare que no enunciado foi dito que serão dadas duas camadas de tinta, ou seja, temos que dobrar a quantidade de galões: