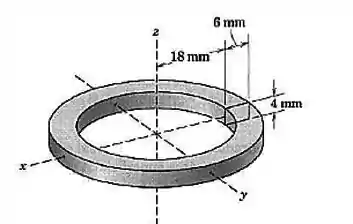
Usando os métodos desta seção determine a área superficial e o volume do corpo formado pela revolução da área retangular por em torno do eixo
Passo 1
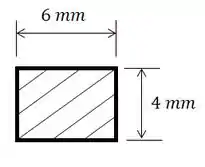
Este corpo é formado quando giramos esta área retangular por em torno do eixo :
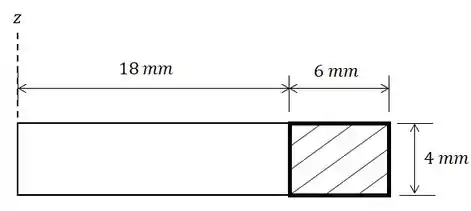
Então, para acharmos a área superficial basta aplicarmos a nossa fórmula de área:
Precisamos calcular e o perímetro da figura.
Passo 2
O é o quanto o centróide do retângulo está afastado do eixo em que a figura gira, neste nosso caso é o eixo . O centróide de um retângulo fica no seu centro geométrico, então vamos ter que:
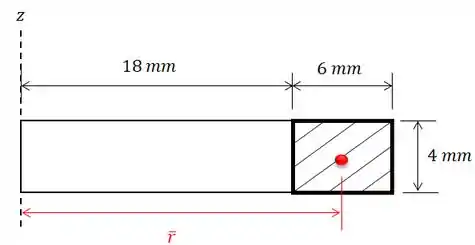
Então, será:
Passo 3
Agora vamos calcular o perímetro do retângulo que dá origem ao nosso corpo:
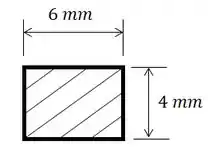
Então, vamos ter que:
Passo 4
Agora sim podemos calcular a área superficial do corpo:
Passo 5
Vamos calcular agora o volume deste corpo. Para isso, precisamos aplicar esta fórmula aqui:
Já sabemos :
Precisamos calcular a área do nosso retângulo:
Então, o volume do corpo é: