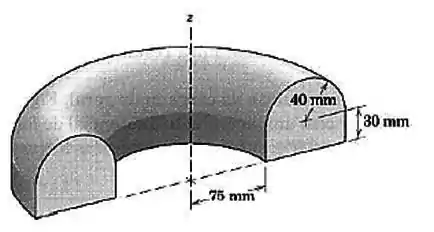
Determine o volume e a área superficial do sólido gerado pela revolução da área mostrada por em torno do eixo
Passo 1
Para achar o volume temos que usar a seguinte equação:
O é a distância do centro da figura até o eixo (que é o eixo em torno do qual a figura gira):
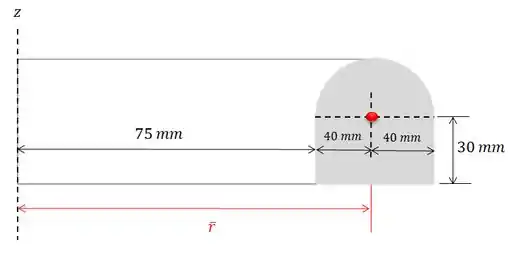
Passo 2
E a área ? Vai ser a soma das áreas do retângulo e do semicírculo:
- Retângulo:
- Semicírculo:
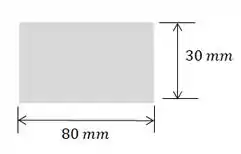
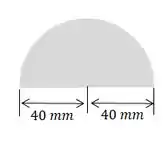
Então, a área total será:
Passo 3
Agora sim podemos calcular o volume do sólido:
Passo 4
Agora precisamos calcular a área superficial do sólido e para isso vamos usar esta fórmula aqui:
O é o perímetro da nossa figura:
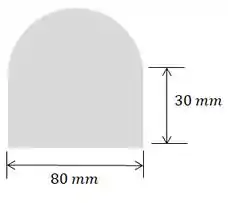
Repare que o perímetro do semicírculo é:
E o perímetro do retângulo fica:
Então, o perímetro total da nossa figura é:
Passo 5
O continua o mesmo:
Então, a área superficial do sólido é:
Resposta
Exercícios de Livros Relacionados
A área de um setor circular é girada de 180° em torno do eixo y. Determine o volume do corpo resultante, o qual é parte de uma esfera.
A caixa d’água AB tem tampa hemisférica e é construída com placas de aço finas. Determine o volume dentro da caixa.
Um anel é gerado ao girar-se a área de um quarto de círculo em torno do eixo x. Determine seu volume.
Determine o volume do material necessário para realizar a moldagem.
Determine a área da superfície interior do pistão de freio. Ele consiste em uma peça completamente circular. Sua seção transversal aparece na figura.