A área de um setor circular é girada de em torno do eixo . Determine o volume do corpo resultante, o qual é parte de uma esfera.
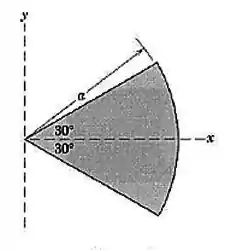
Passo 1
Primeiro vamos calcular a distância do centróide até o eixo
Para isso, vamos usar a fórmula de centróide da área de um setor circular:
O ângulo é de , mas temos que passar isso para radianos. Vamos fazer uma regra de sabendo que corresponde a radianos:
Agora sim podemos calcular a coordenada do centróide:
Passo 2
Esse vai ser nada mais nada menos que o nosso
E quando vale a nossa área?
Basta ver que esse setor circular tem uma abertura de , assim, a área dele vai da área de um círculo:
Passo 3
Agora basta a gente usar a formula:
Resposta
Exercícios de Livros Relacionados
A área de um setor circular é girada de 180° em torno do eixo y. Determine o volume do corpo resultante, o qual é parte de uma esfera.
A caixa d’água AB tem tampa hemisférica e é construída com placas de aço finas. Determine o volume dentro da caixa.
Um anel é gerado ao girar-se a área de um quarto de círculo em torno do eixo x. Determine seu volume.
Determine o volume do material necessário para realizar a moldagem.
Determine a área da superfície interior do pistão de freio. Ele consiste em uma peça completamente circular. Sua seção transversal aparece na figura.