Calcule o peso do fundido de alumínio mostrado. O sólido é gerado pela revolução de da área trapezoidal mostrada, em torno do eixo Considere que a massa específica do alumínio é de .
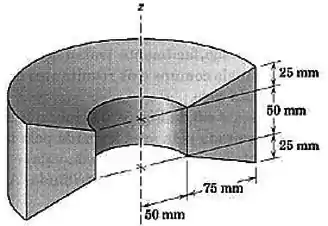
Passo 1
A área que vamos usar pra gerar o volume é dada abaixo:
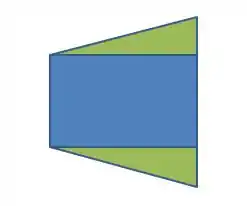
Mas veja: Ela pode ser dividida em duas regiões: A verde e a azul.
Sabe como podemos usar isso ao nosso favor? O volume do sólido vai ser a soma dos volumes gerados das duas regiões:
Passo 2
Vamos começar com a parte azul. Vamos usar:
A área é a área do retângulo:
E vai ser a distância do centro do retângulo até o eixo em torno do qual a figura gira, neste caso o eixo :
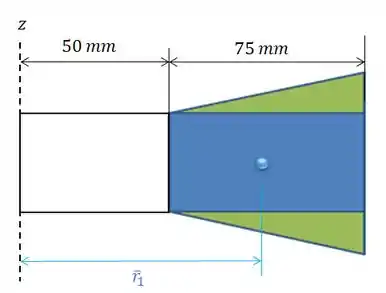
Então:
Assim:
Vamos passar isso para metros, pois temos que calcular o peso:
Passo 3
E a parte verde? Vai ser dada por:
Perceba que multiplicamos por dois, pois são dois triângulos verdes!!!
O vai ser a distância até o centróide do triângulo:
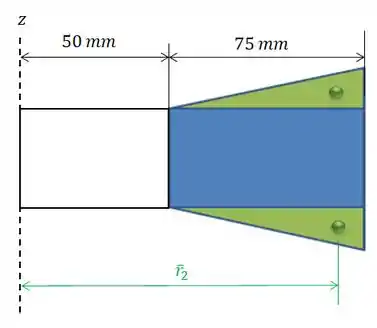
Perceba que, na posição que foi colocado, teremos que usar da altura nos cálculos:
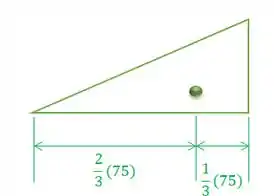
E a área de um dos triângulos será:
Agora podemos calcular o volume do sólido gerado pela revolução dos triângulos:
Passando isso para , temos:
Passo 4
Agora é só somar:
Passo 5
Mas não é nossa resposta final, porque queremos saber o peso do sólido. Sabendo que a massa específica do alumínio é , temos que a massa do sólido será de:
Então, o peso será igual a: