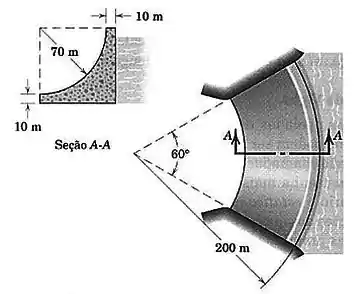
Calcule a massa de concreto necessária para construir a represa em arco mostrada. O concreto uma massa específica de .
Passo 1
Para resolver esta questão precisamos encontrar o volume de concreto que será usado nesta represa e para isso vamos usar a nossa fórmula:
Vamos usar esta fórmula porque se você reparar a nossa figura não gira em torno do eixo, ela gira somente .
O é a distância do centróide da figura até o eixo em torno da qual ela gira. E é a área da figura.
Mas que figura é esta que estamos falando? É a figura que ao girarmos em tono do eixo vai dar origem a nossa represa, ou seja, é a seção transversal da represa.
Então, a nossa figura tem esse formato aqui:
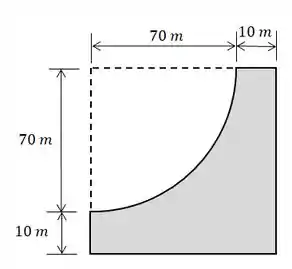
O que isso te lembra? Repare que temos um quadrado e dele retiramos de círculo, ou seja, temos aqui um corpo composto de duas figuras.
Para
Vamos primeiro calcular a equação da senóide:
Onde é a equação da senóide, no modelo: . Vamos usar o ponto final:
Pela função, conseguimos perceber que . Assim:
Passo 2
Vamos começar achando o centróide desta figura. Para isso temos que posicionar o eixo em torno do qual a figura gira (vamos chamar de eixo ):
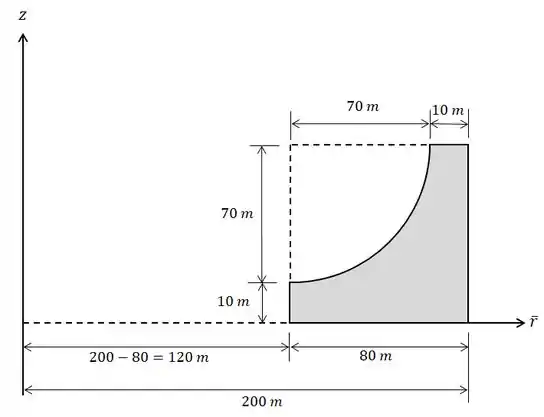
Repare na figura que foi dada no enunciado que o final da represa está distante do eixo!
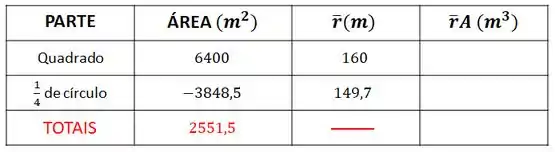
Agora vamos achar a área de cada parte que compõe a nossa figura:
E o de círculo cujo raio é de é:
Não esqueça que temos que tratar a área de de círculo como negativa, pois estamos retirando esta área da área total do quadrado.
Então, a área total da figura é:
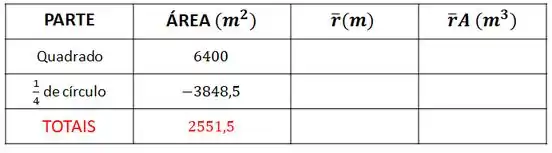
Lembra da nossa tabela? Vamos montá-la para facilitar as coisas:
Passo 3
Agora temos que achar a coordenada do centróide de cada parte que compõe a nossa figura. Vamos começar pelo quadrado:
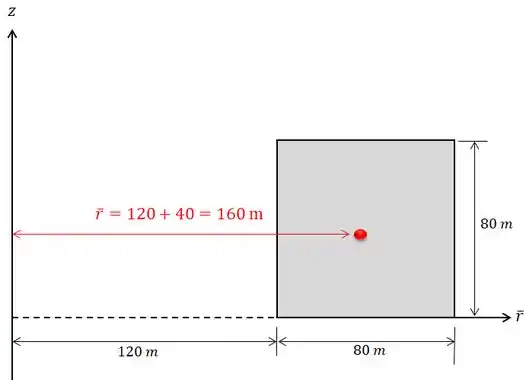
Sabendo que o centróide do quadrado fica no seu centro geométrico, temos que:
E o centróide do de círculo se calcula com a seguinte fórmula:
Somando a isso os até chegar o eixo, vamos ter que:
Vamos colocar isso na nossa tabela:
Passo 4
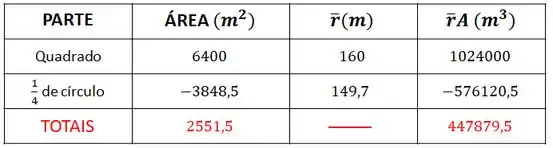
Agora temos que multiplicar a área de cada parte pela sua respectiva coordenada :
E:
Agora precisamos somar esses dois valores:
Vamos colocar isso na nossa tabela também:
Beleza?
Passo 5
Agora é só aplicarmos a fórmula do centróide para corpos compostos:
Pronto, já achamos a distância do centróide da nossa figura até o eixo em torno da qual ela gira.
Perceba que neste processo achamos também a área total da nossa figura:
Então, já temos tudo para achar o volume de concreto da represa.
Passo 6
Para calcular o volume, vimos que vamos precisar usar esta fórmula aqui:
Onde esse ângulo corresponde ao ângulo que a figura gira em torno do eixo, ou seja, ele vale . Mas é necessário passar para radianos antes!
Para isso vamos fazer uma regra de sabendo que corresponde a radianos:
Agora sim podemos achar o volume:
Mas isso ainda não é a nossa resposta final!
Passo 7
Queremos saber a massa de concreto que será necessária para construir a represa, para isso temos que saber que:
Onde é a massa específica do concreto, a qual vale .
Então:
Podemos escrever assim: