Um método padrão para a determinação de glucose em soro tem desvio padrão de . Se é uma boa aproximação para , quantas determinações precisarão ser feitas para que a média da análise da amostra esteja entre:
- da média real das vezes?
- da média real das vezes?
- da média real das vezes?
Passo 1
Nesse exercício, precisamos comparar o valor da média encontrada no método utilizado com o valor da média real. Ou seja:
Isso é um indicativo que termos que usar ou teste z ou teste t, que são os dois métodos que comparam uma média com um valor real. Entretanto, como o exercício já nos diz que o desvio padrão da amostra () pode ser aproximado ao desvio padrão da população (), isso é um indicativo que devemos usar o teste z e não o teste t, uma vez que o teste z é feito sob essa hipótese, de que é suficientemente próximo de .
Passo 2
Para definir quantas amostras serão necessárias, usaremos a fórmula abaixo:
O valor de e não foi dado, entretanto, foi dado a diferença entre eles em cada item, portanto usaremos essa diferença no denominador da nossa expressão.
O valor de nós pegaremos da tabela de z:
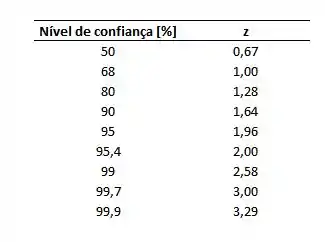
Para cada nível de confiança.
Por fim, o valor de foi dado e é . Portanto, temos apenas uma variável na equação, que é justamente o número de amostras que precisaremos encontrar.
Passo 3
Sendo assim, para o primeiro item teremos:
Jogando tudo na expressão:
Calculando , termos:
Como o número de replicatas deve ser inteiro, teremos então .
Passo 4
Para o segundo item:
Jogando tudo na expressão:
Calculando , termos:
Como o número de replicatas deve ser inteiro, teremos então .
Passo 5
Por fim, para o terceiro item:
Jogando tudo na expressão:
Calculando , termos:
Como o número de replicatas deve ser inteiro, teremos então .