Exercícios Resolvidos de Trabalho de uma força

Enunciado

Integral Definida

Uma corrente de 1,5 m de comprimento pesa 10 N e está dependurada em um

teto. Encontre o trabalho necessário para levantar a extremidade inferior da

corrente até o seu ponto médio (ponto médio da corrente esticada).

Passo 1

Primeira coisa a se fazer é definir as orientações dos eixos. Nesse caso, vamos definir o eixo na vertical, orientado para baixo e com a origem no ponto em que a corrente está presa no teto.

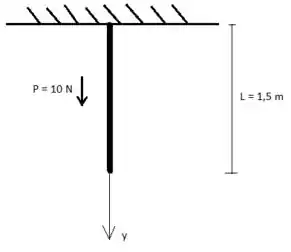
Passo 2

Agora vamos escrever quanto vale o peso de cada pedacinho infinitesimal da corrente, porque vamos precisar desse peso pra calcular o trabalho necessário pra conseguir erguer a corrente. Então cada pedacinho de comprimento pesa . Pois repare que foi feita uma regra de três:

Passo 3

E o deslocamento de cada pedacinho vai ser dado por: . Pois repare que a extremidade inferior do fio terá o deslocamento máximo que é igual a metade do comprimento do fio e o pedacinho que dista do teto do comprimento total do fio terá o deslocamento nulo.

Passo 4

Então, podemos escrever a expressão do trabalho como:

Os extremos de integração são esses pois os pedacinhos de fio nesse intervalo são os únicos que se deslocam e portanto entram na conta do trabalho. E a força necessária pra erguê-los é igual ao peso desses pedacinhos que serão erguidos, que nós já escrevemos em função de sua posição no fio.