Suponha que o gás contido em um cilindro com área transversal esteja sendo comprimido por um pistão. Se for a pressão do gás em e o volume em , o trabalho realizado na compressão do gás, do estado até o estado é dado pela equação:
Use essa integral para determinar o trabalho realizado ao comprimir o gás de a , se e e obedecem à lei dos gases , para processos adiabáticos.
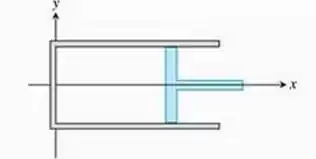
(Dica: Nas coordenadas sugeridas pela figura, . A força contra o pistão é )
Passo 1
Bem, ele quer o trabalho realizado para comprimir um gás de dado volume e dada pressão até outro estado. A integral a ser usada, ele já definiu no enunciado e é essa aqui embaixo:
Além disso, ele definiu a relação entre e nesse processo.
Nesse tipo de questão, o mais difícil é que, se não é constante, ou seja, se varia com o volume, temos que escrever em função de para poder integrar, já que a integral está definida para .
Nesse caso, ele deu a relação entre e . Então é essa relação que temos que usar para relacionar os dois e escrever em função de .
Passo 2
A primeira coisa que eu vou fazer é justamente escrever em função de .
Ele diz que:
Então:
Beleza, tá tudo muito bom, mas como achar essa constante ?
Repara que no estado inicial do gás, ele dá as duas condições do gás e . Logo, temos como substituir na fórmula e encontrar , não é mesmo?
Olha aqui:
Substituindo na fórmula:
Passo 3
Agora eu tenho que substituir na integral. Temos que lembrar que como a nossa variável de integração é , os limites de integração devem ser dados em função de .
Temos, do enunciado:
Logo:
- ''Passo 4
Resolvendo a integral:
O trabalho realizado pelo sistema é negativo porque se trata de uma compressão.
- ''