Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Transformada de Função vezes Exponencial

Ver Teoria
Exercício 1012345678911

Enunciado

Determine a transformada de Laplace da função f ( t )   =   e 2 t ( s e n ( 3 t )   -   s e n ( 2 t ) ) .  

  3 s 2 - 4 s + 4 - 2 s 2 - 4 s + 8

  3 s 2 - 4 s + 9 + 2 s 2 - 4 s + 8

  3 s 2 - 4 s + 13 - 2 s 2 - 4 s + 8

  3 s 2 - 4 s + 13 + 2 s 2 - 4 s + 8

Passo 1

Opaa, vamos lá! A questão quer que a gente calcule a transformada de Laplace da função:

f ( t )   =   e 2 t ( s e n ( 3 t )   -   s e n ( 2 t ) )  

Fazendo a distributiva (também conhecida como chuveirinho) com a função exponencial, temos:

f t = e 2 t sen ⁡ ( 3 t ) - e 2 t sen ⁡ ( 2 t )

Agora, vamos olhar na tabela de transformadas de Laplace qual função mais se parece com o que a gente quer.

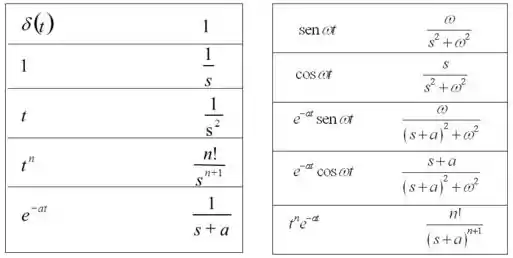
Bom, a função que mais se parece é e - a t sen ⁡ w t .

Vamos fazer a transformada do primeiro termo:

L e 2 t sen ⁡ 3 t = 3 s - 2 2 + 3 2 = 3 s 2 - 4 s + 4 + 9 = 3 s 2 - 4 s + 13

Agora, vamos fazer a transformada do segundo termo:

L e 2 t sen ⁡ 2 t = 2 s - 2 2 + 2 2 = 2 s 2 - 4 s + 4 + 4 = 2 s 2 - 4 s + 8

Juntando os dois termos, teremos:

L f t = 3 s 2 - 4 s + 13 - 2 s 2 - 4 s + 8

Resposta

L f t = 3 s 2 - 4 s + 13 - 2 s 2 - 4 s + 8