Encontre ou seja a transformada de Laplace da função onde a função cosseno hiperbólico de , é assim definida .

.

( )

( )

( )

( )

( )

Opa, vamos lá. A questão quer que a gente calcule a transofmada de Laplace para a nossa função:

Repara só que ela nos dá uma dica:

Logo,

Vamos substituir isso na nossa função:

Bom, agora para encontrarmos a transformada de Laplace, podemos olhar a tabela de transformadas, em especial esse pedacinho aqui dela:

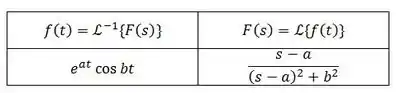
Olha, é bem o que a gente quer, né?

Então nossa transformada vai ficar:

Bom, juntando essas frações, teremos: