Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Transformada de Função vezes Exponencial

Ver Teoria
Exercício 1112345678910

Enunciado

Determine a Transformada de Laplace de f t = 6 e - 3 t - t 2 + 2 t - 8   e indique a única resposta correta:

      6 s + 3 - 2 s 3 + 2 s 2 - 8 s

      6 s + 3 + 1 s 3 + 2 s - 8 s

      6 s 2 + 3 + 1 s 3 + 2 s - 8 s

      6 s - 3 + 1 s 3 + 2 s - 8 s

      6 s + 3 - 2 s 3 + 2 s 2 + 8 s

Passo 1

Fala aí!! Essa questão quer a transformada de Laplace da nossa função:

f t = 6 e - 3 t - t 2 + 2 t - 8

Bom, vamos ver as funções que a gente tem na tabela de transformadas de Laplace:

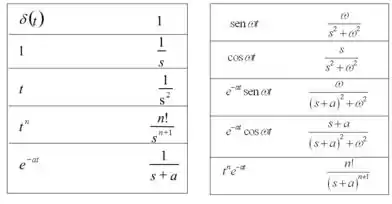
Agora, vamos comparar termo a termo.

1) L e - 3 t = 1 s + 3 (Nesse caso, a = 3 )

2) L t 2 = 2 ! s 2 + 1 = 2 s 3

3)   L t = 1 s 2

4)   L 8 = 8 1 s = 8 s

Pronto, agora que já sabemos as transformadas de Laplace de todos os termos, podemos substituir na expressão.

L f t = L 6 e - 3 t - t 2 + 2 t - 8 = 6 1 s + 3 - 2 s 3 + 2 s 2 - 8 s

Resposta

L f t = 6 s + 3 - 2 s 3 + 2 s 2 - 8 s