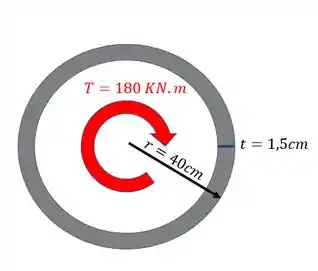
Abaixo é dado um tubo de parede fina com seção circular. Sabendo que ele foi sujeito ao torque mostrado, determine o valor da tensão cisalhante média para esse tubo.
Passo 1
Como podemos notar, se trata de um problema relacionando a tubos de paredes finas quando ocorre torção dos elementos, sabemos que nesse tipo de questão devemos usar a fórmula
Alguns valores determinamos facilmente, por exemplo o valor de , que é dado no enunciado
Também determinamos facilmente o valor da espessura do nosso tubo, que é dada por
Agora precisamos determinar o valor da área média do nosso tubo.
Passo 2
Precisamos agora determinar a nossa área média, como sabemos a área média é dada pela área da figura quando tomamos como medida a metade de espessura de cada lado, como mostra a figura baixo, ou seja, podemos definir a nossa área média como
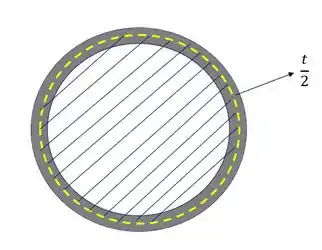
Lembrando que
Substituindo isso na nossa equação principal teremos que