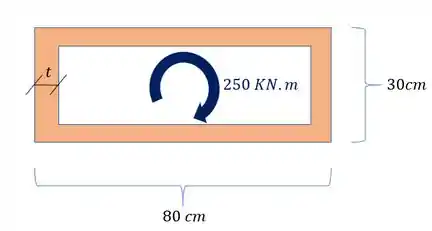
Deseja-se construir um tubo de parede fina com espessura das paredes constantes. Sabendo que o tubo é retangular e possui as dimensões mostradas abaixo, determine o valor da espessura do tubo sabendo que o material que ele é feito possui tensão de cisalhamento admissível de e o local em que ele será usado apresentará esforços torsores de
OBS:. PARA EFEITO DE CÁLCULO. Como consideramos espessuras de paredes finas para o nosso caso, qualquer valor de espessura que esteja sujeito a equação pode ser desprezado por representar um valor muito pequeno.
Passo 1
Como podemos notar, se trata de um problema relacionando a tubos de paredes finas quando ocorre torção dos elementos, sabemos que nesse tipo de questão devemos usar a fórmula
Alguns valores determinamos facilmente, por exemplo o valor de , que é dado no enunciado
Também determinamos facilmente o valor da tensão cisalhante média, como queremos a espessura máxima que o nosso tubo pode ter, queremos exatamente o valor limite que poderia causar o rompimento da peça, como isso temos que fazer
Agora para determinarmos os outros valores devemos tomar um certo cuidado, pois estamos falando que tanto a área média quanto a própria espessura são valores que não conhecemos, vamos analisar então cuidadosamente.
Passo 2
Precisamos agora determinar a nossa área média, como sabemos a área média é dada pela área da figura quando tomamos como medida a metade de espessura de cada lado, como mostra a figura baixo, ou seja, podemos definir a nossa área média como
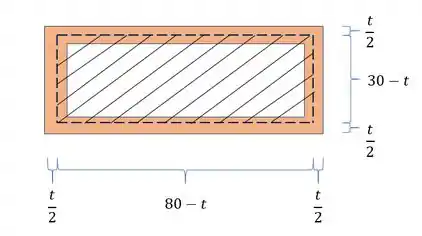
Substituindo isso na nossa equação principal teremos que
Como temos no nosso enunciado que podemos desprezar o valor de teremos a seguinte equação
Como sabemos a nossa equação do segundo grau apresentará duas soluções, e a resposta mais adequada será a que possuir o menor valor de espessura, solucionando a nossa equação teremos que
Logo a espessura mais fina que o nosso tubo poderá ter é de
Como queremos trabalhar com valores usuais para quem fará o tubo, aproximaremos o valor para meio centímetro, ou seja
Resposta
(valor calculado)
(valor usual)