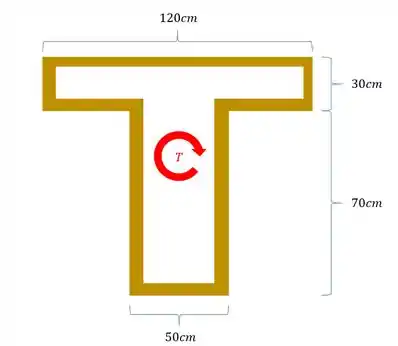
Exercícios Resolvidos de Tubos de Paredes Finas

Enunciado

Um tubo de parede fina possui seção T como mostrado na figura. Sabe-se que a tensão cisalhante admissível desse material é de . Também sabemos que a espessura da parede é constante por todo o tubo e vale 0,1mm. Sabendo isso determine o valor do toque máximo que podemos aplicar nessa peça sem que ela rompa.

Passo 1

Como podemos notar, se trata de um problema relacionando a tubos de paredes finas quando ocorre torção dos elementos, sabemos que nesse tipo de questão devemos usar a fórmula

Alguns valores determinamos facilmente, por exemplo o valor do , que é dado no enunciado

Também determinamos facilmente o valor da espessura do nosso tubo, que é dada por

Agora precisamos determinar o valor da área média do nosso tubo.

Passo 2

Para determinarmos a área média do nosso tubo, precisaremos definir 2 regiões de cálculo para não errarmos bobeira, então vamos lá.

Primeiro vamos fazer a divisão das regiões.

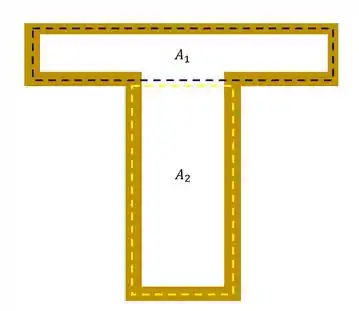
Olhando as medidas dos lados que farão parte da área média teremos que

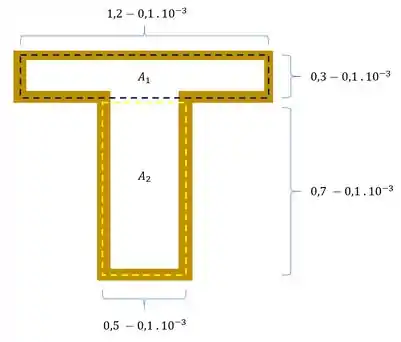
Lembrando que

Teremos que as áreas serão

Logo a área média será

Substituindo isso na nossa equação principal teremos que

Resposta

Exercícios de Livros Relacionados

Placas quadradas, cada uma com 16 m m de espessura, podem ser soldadas juntas de dois modos distintos, como mostrado, para formar um tanque cilíndrico de ar comprimido. Sabendo-se que a tensão normal

Determine o torque T que pode ser aplicado ao tubo retangular se a tensão de cisalhamento média não pode ultrapassar 84M P a . Despreze as concentrações de tensão nos cantos. As dimensões médias do tu

O tubo de 2m de comprimento é feito de um material elástico-plástico como mostra a figura. Determine o torque aplicado T que submete o material da borda externa do tubo a uma deformação por cisalhamen

Um torque de intensidade T = 12k Nm é aplicado à extremidade de um tanque que contém ar comprimido sob uma pressão de 8M P a . Sabendo que o tanque tem um diâmetro interno de 180m m e uma espessura de

Para o tanque do problema 7,117 , determine a maior pressão manométrica admissível, sabendo que a tensão normal perpendicular à solda é 18k s i e a tensão de cisalhamento admissível paralela à solda é