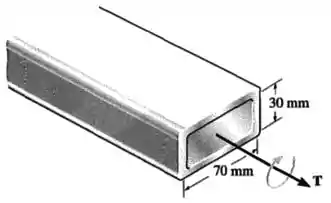
O tubo de aço inoxidável 304 tem espessura de . Se a tensão de cisalhamento admissível for , determine o torque máximo que ele pode transmitir. Calcule também o ângulo de torção de uma extremidade do tubo em relação à outra se o tubo tiver de comprimento. Despreze as concentrações de tensão nos cantos. As dimensões médias são mostradas na figura.
Dados: .
Passo 1
O que está acontecendo?
O tubo de paredes finas retangular tem dimensões médias de e . Consequentemente, ele tem uma área média e um perímetro da área média :
Além disso, ele possui:
- Uma espessura constante ;
- Uma tensão de cisalhamento admissível ;
- Um módulo de elasticidade transversal ;
- & um comprimento .
Devido a um torque aplicado, ele vai sofrer uma tensão de cisalhamento média e um ângulo de torção que vão ser dados pelas fórmulas:
E o que é que o exercício quer?
Primeiro, ele quer saber qual é o torque máximo que pode ser aplicado de tal forma que a tensão de cisalhamento média na peça não ultrapasse a admissível:
Em seguida, ele quer que a gente use o valor encontrado para para calcular o ângulo de torção no tubo correspondente.
Passo 2
Então para encontrar o torque máximo, vamos pegar a nossa condição de projeto:
E desenvolvê-la, até que seja possível isolar o torque .
A primeira coisa que podemos fazer é aplicar a fórmula da tensão de cisalhamento média para tubos de paredes finas:
Fazendo isso, a nossa condição de projeto fica assim:
Isolando o torque , temos que:
Finalmente, substituindo os valores:
- ;
- ;
- & ,
Encontramos que:
Reescrevendo isso em , temos que:
Ou seja, é o torque máximo que pode ser transmitido por esse tubo.
Passo 3
Agora, para a segunda parte do exercício, vamos calcular o ângulo de torção nesse tubo de paredes finas aplicando a sua fórmula:
No caso do nosso tubo, a espessura é constante: ela é sempre igual à ao longo de todo o perímetro .
Então podemos colocar a espessura do lado de fora da integral:
Em seguida, temos que a integral de todos os pedaços infinitesimais do perímetro da área média vai ser o próprio perímetro da área média :
Dessa forma, o nosso ângulo de torção vai ficar assim:
Substituindo os valores:
- ;
- ;
- ;
- ;
- ;
- & ,
E calculando tudo, encontramos que:
A maioria dos professores prefere que os resultados finais sejam dados em graus (), então vamos fazer a conversão do ângulo acima de radianos para graus!
Para tanto, podemos perceber que:
Ou seja:
Substituindo isso no ângulo de torção encontrado, temos que:
Calculando isso, encontramos nossa resposta para a segunda e última parte do exercício: