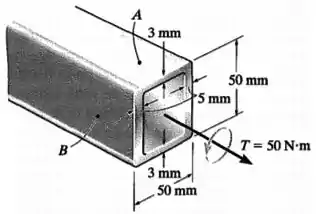
Um tubo com as dimensões mostradas na figura é submetido a um torque . Despreze as concentrações de tensão em seus cantos, determine a tensão de cisalhamento média no tubo nos pontos e .
Passo 1
O que está acontecendo?
O tubo de paredes finas retangular possui dimensões conforme a figura abaixo:
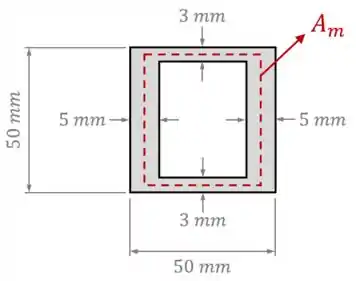
Da figura, conseguimos ver como o tubo possui dimensões médias de e de :
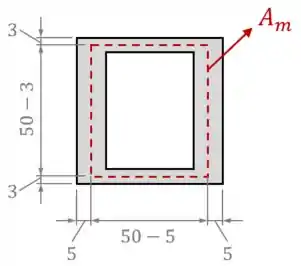
Consequentemente, o tubo possui uma área média :
Além disso, também da figura, conseguimos ver que o tubo possui, na região do ponto , uma espessura e, na região do ponto , uma espessura .
Um torque é aplicado no tubo.
E o que é que o exercício quer?
Ele quer que a gente determine as tensões de cisalhamento médias nos pontos e do tubo, que vão ser dadas pela fórmula:
Passo 2
Então primeiro, vamos começar calculando a tensão de cisalhamento média no ponto .
Aplicando a fórmula de para , temos que:
Substituindo os valores:
- ;
- ;
- & ,
- ;
- ;
- & ,
Encontramos que:
Mas, como é o mesmo que , isso significa que:
Passo 3
Em seguida, vamos calcular a tensão de cisalhamento média no ponto .
Aplicando a fórmula de para , temos:
Substituindo:
Encontramos que:
E assim terminamos o exercício!