Um determinado fabricante produz implantes mamários utilizando gel de silicone. Os dados a seguir se referem a tensão de ruptura desses implantes e foram obtidos através de testes físicos realizados com uma amostra de tamanho n=20:
![]()
Com base nesses dados obtenha os quartis Q1,Q2 e Q3.
Foi apresentada a seguinte solução:

Posição (Q2)=
Posição (Q1) =
Posição (Q3) =
a) Algo está errado nessa solução. O que é?
b) Qual a solução correta?
Passo 1
a) E aí? Está errada a solução? Sim!
Está errada pois ele esqueceu de ordenar em ordem crescente! Esse é o primeiro passo, depois isso as coisas desandaram.
Passo 2
Vamos colocar na ordem crescente e calcular os quartis.
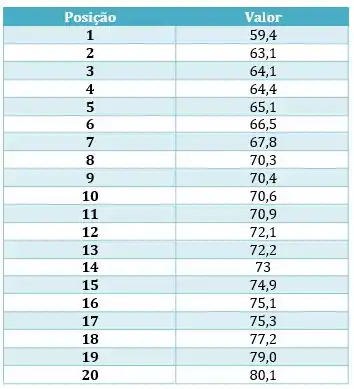
Passo 3
Agora vamos calcular os quartis.
- Q2
Sabemos que Q2 é a mediana, neste caso como temos um total par de números
Passo 4
- Q1
Temos um total de 20 posições, portanto
Faremos
Portanto o Q1 está entre a posição 5 e 6.
Fazendo a interpolação
Passo 5
- Q3
Para o cálculo de Q3 faremos primeiro
Isso quer dizer que Q3 está entre o 15 e o 16.
Fazendo a interpolação