A tabela de dados brutos a seguir reporta, o número de linhas telefônicas por 1000 habitantes em cada estado do Brasil, em 2001.
b) Determine os seus quartis
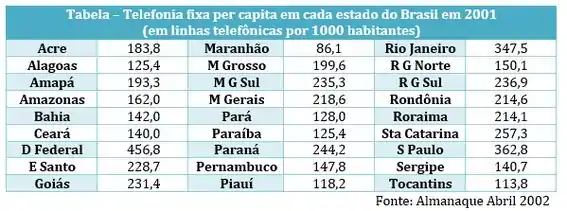
Passo 1
Bom, a primeira coisa que devemos fazer para determinar os quartis é colocar nossos dados em ordem crescente:
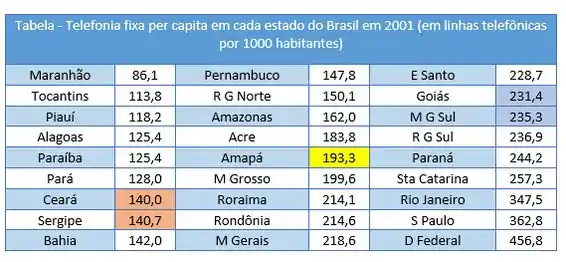
Passo 2
Temos que .
- Para encontrar Q1 faremos:
- Para encontrar Q3 faremos:
Isso quer dizer que Q1 vai estar entre a posição 7 e a posição 8, fazendo a interpolação:
Passo 3
Isso quer dizer que Q3 vai estar entre a posição 20 e a posição 21. Fazendo a interpolação: